Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 2 - Hình học 9 — Không quảng cáo

Đề bài

Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, R, S lần lượt là trung điểm của các cạnh AB, BC, CD và DA.

a. Chứng minh rằng bốn điểm M, N, R, S thuộc cùng một đường tròn.

b. Cho $AC = 24cm, BD = 18cm.$ Tính bán kính đường tròn ngoại tiếp tứ giác MNRS.

Lời giải chi tiết

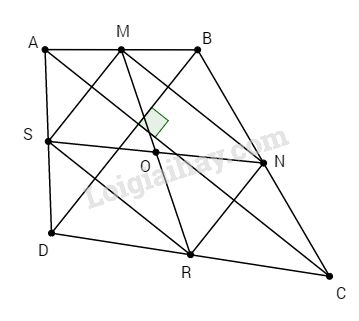
a. Ta có: M, N lần lượt là trung điểm của AB và BC (gt) nên MN là đường trung bình của ∆ABC.

Do đó : MN // AC (1)

Tương tự SR là đường trung bình của ∆ADC nên SR // AC  (2)

Từ (1) và (2) ⇒ MN // RS // AC (3)

Chứng minh tương tự ta có: MS // NR // BD  (4)

Từ (3) và (4) ⇒ MNRS là hình bình hành (các cạnh đối song song)

Mặt khác AC ⊥ BD (gt) ⇒ MN ⊥ MS nên hình bình hành MNRS là hình chữ nhật.

Gọi O là giao điểm của hai đường chéo MR và NS ta có:

OM = ON = OR = OS

Chứng tỏ bốn điểm M, N, R, S thuộc cùng một đường tròn tâm O.

b. Ta có: MN là đường trung bình của ∆ABC (cmt), ta có:

$MN = {1 \over 2}AC = {1 \over 2}.24 = 12\,\left( {cm} \right)$

Tương tự: $MS = {1 \over 2}BD = 9\,\left( {cm} \right)$

Lại có ∆MNS vuông tại M (cmt) ta có:

$SN = \sqrt {M{N^2} + M{S^2}}$$\;= \sqrt {{{\left( {12} \right)}^2} + {{\left( 9 \right)}^2}}  = 15\left( {cm} \right)$

Vậy đường tròn ngoại tiếp tứ giác MNRS có tâm O và bán kính là

${{SN} \over 2} = {{15} \over 2} = 7,5\,\left( {cm} \right)$