Đề kiểm tra 15 phút Toán 6 Cánh diều - Đề số 3 — Không quảng cáo

Phương pháp giải :

Suy luận từ giả thiết đề bài.

Lời giải chi tiết :

Nếu \(a < b\) và \(b < c\) thì \(a < c\).

Phương pháp giải :

Chọn đáp án minh họa tính chất kết hợp của phép cộng.

Lời giải chi tiết :

Tính chất kết hợp của phép cộng là: \(\left( {a + b} \right) + c = a + \left( {b + c} \right);\)

Phương pháp giải :

Quy tắc bỏ dấu ngoặc:

Khi bỏ dấu ngoặc có dấu $'' - ''$ đằng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc: dấu \('' + ''\) chuyển thành dấu \('' - ''\) và dấu \('' - ''\) chuyển thành dấu \('' + ''\).

Khi bỏ dấu ngoặc có dấu \('' + ''\) đằng trước thì dấu các số hạng trong ngoặc vẫn được giữ nguyên.

Lời giải chi tiết :

$\begin{array}{l}5-\left( {4-7 + 12} \right) + \left( {4-7 + 12} \right)\\ = 5 - 4 + 7 - 12 + 4 - 7 + 12\\ = 5 - 4 + 4 + 7 - 7 - 12 + 12\\ = 5 - \left( {4 - 4} \right) + \left( {7 - 7} \right) - \left( {12 - 12} \right)\\ = 5 - 0 + 0 - 0\\ = 5\end{array}$

Phương pháp giải :

- Chọn ra các số nguyên âm trong các phần tử thuộc tập hợp \(C.\)

- Viết tập hợp \(D\) gồm các phần tử là các số vừa tìm được.

Lời giải chi tiết :

Ta có \(C = \left\{ { - 3; - 2;0;1;6;10} \right\}\) có các số nguyên âm là \( - 3; - 2\). Nên tập hợp \(D = \left\{ { - 3; - 2} \right\}.\)

Phương pháp giải :

Cộng hai số nguyên dương chính là cộng hai số tự nhiên.

Lời giải chi tiết :

Ta có \(\left( { + 25} \right) + \left( { + 15} \right) = 25 + 15 = 40.\)

Phương pháp giải :

Sử dụng khái niệm bội và ước của một số nguyên:

Nếu $a,b,x \in Z$ và $a = b.x$ thì $a \vdots b$ và $a$  là một bội của $b;b$ là một ước của $a$

Lời giải chi tiết :

Bội của $6$ là số $0$ và những số nguyên có dạng \(6k\,\left( {k \in {Z^*}} \right)\)

Các bội của $6$ là: \(0;\;\,6;\, - 6;\;\,12;\, - 12;\,...\)

Phương pháp giải :

- Tích của hai số nguyên trái dấu là số nguyên âm.

- Tính của hai số nguyên cùng dấu là số nguyên dương.

Lời giải chi tiết :

Tích ba số nguyên âm là một số nguyên âm.

Tích hai số nguyên âm với một số nguyên dương là một số nguyên dương

Phương pháp giải :

Số nguyên dương là các số tự nhiên khác \(0\).

Lời giải chi tiết :

Nếu \(a\) là số nguyên dương thì: \(a > 0\).

Phương pháp giải :

\(10\) là bội của \(2a + 5\) nghĩa là \(2a + 5\) là ước của \(10\)

- Tìm các ước của \(10\)

- Lập bảng tìm \(a,\) đối chiếu điều kiện và kết luận.

Lời giải chi tiết :

Vì \(10\) là bội của \(2a + 5\) nên \(2a + 5\) là ước của \(10\)

\(U\left( {10} \right) = \left\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}\)

Ta có bảng:

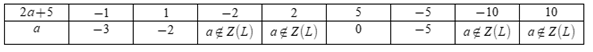
Mà \(a < 5\) nên \(a \in \left\{ { - 3; - 2;0; - 5} \right\}\)

Vậy có \(4\) giá trị nguyên của \(a\) thỏa mãn bài toán.

Phương pháp giải :

Biến đổi biểu thức \({n^2} - 7\) về dạng \(a.\left( {n + 3} \right) + b\) với \(b \in Z\) rồi suy ra \(n + 3\) là ước của \(b\)

Lời giải chi tiết :

Ta có:\({n^2} - 7 = {n^2} + 3n - 3n - 9 + 2\)\( = n\left( {n + 3} \right) - 3\left( {n + 3} \right) + 2\)\( = \left( {n - 3} \right)\left( {n + 3} \right) + 2\)

Vì \(n \in Z\) nên để \({n^2} - 7\) là bội của \(n + 3\) thì \(2\) là bội của \(n + 3\) hay \(n + 3\) là ước của \(2\)

\(Ư\left( 2 \right) = \left\{ { \pm 1; \pm 2} \right\}\) nên \(n + 3 \in \left\{ { \pm 1; \pm 2} \right\}\)

Ta có bảng:

Vậy \(n \in A = \left\{ { - 5; - 4; - 2; - 1} \right\}\)

Do đó tổng các phần tử của \(A\) là \(\left( { - 5} \right) + \left( { - 4} \right) + \left( { - 2} \right) + \left( { - 1} \right) =  - 12\)