Đề kiểm tra giữa học kì 1 Toán 6 Cánh diều - Đề số 3
Đề bài
Chọn câu đúng:
-
A.
Diện tích hình bình hành bằng nửa tích của cạnh đáy nhân với chiều cao.
-
B.
Diện tích hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Diện tích hình bình hành bằng hiệu của cạnh đáy và chiều cao.
Tìm tập hợp các bội của $6$ trong các số: $6;15;24;30;40$.
-
A.
$\left\{ {15;24} \right\}$
-
B.
$\left\{ {24;30} \right\}$
-
C.
$\left\{ {15;24;30} \right\}$
-
D.
$\left\{ {6;24;30} \right\}$
Tìm số tự nhiên $x$ thỏa mãn: $7+x=362$.
-
A.
300
-
B.
355
-
C.
305
-
D.
362
Tìm $x$ biết: \(65 - {4^{x + 2}} = 1\)
-
A.
$5$
-
B.
$4$
-
C.
$3$
-
D.
$1$
-
A.
Hình a
-
B.
Hình b
-
C.
Hình c
-
D.
Hình a và Hình c
Tập hợp số tự nhiên được kí hiệu là
-
A.
\(N\)
-
B.
\({N^*}\)
-
C.
\(\left\{ N \right\}\)
-
D.
\(Z\)
\({7^2}{.7^4}:{7^3}\) bằng
-
A.
\({7^1}\)
-
B.
\({7^2}\)
-
C.
\({7^3}\)
-
D.
\({7^9}\)
Khi phân tích 104 thành tích các thừa số nguyên tố thì số mũ của thừa số 2 là
-
A.
2
-
B.
1
-
C.
3
-
D.
4
Giá trị của biểu thức \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\) bằng
-
A.
$140$
-
B.
$60$
-
C.
$80$
-
D.
$40$
-
A.
\(MQ = NR\)
-
B.
\(MH = RQ\)
-
C.
\(MN = HR\)
-
D.
\(MH = MQ\)
Số $x$ là ước chung của số $a$ và số $b$ nếu:
-
A.
$x \in $Ư$\left( a \right)$ và $x \in B(b)$
-
B.
$x \subset Ư(a)$và $x \subset Ư(b)$
-
C.
$x \in $Ư\(\left( a \right)\) và $x \in $Ư\(\left( b \right)\)
-
D.
$x \notin Ư(a)$ và $x \notin Ư(b)$
-
A.
Hình con sao biển có trục đối xứng
-
B.
Hình chiếc lá có trục đối xứng
-
C.
Hai hình đều có trục đối xứng.
-
D.
Không có hình nào có trục đối xứng
Thay dấu * để được số nguyên tố $\overline {3*} $:
-
A.
$7$
-
B.
$4$
-
C.
$6$
-
D.
$9$
Trong những số sau, có bao nhiêu số chia hết cho 5?
10005459, 12345, 1254360, 1234544, 155498
-
A.
2
-
B.
3
-
C.
4
-
D.
5
-
A.
\(AB = AC\)
-
B.
\(AC = DO\)
-
C.
\(AC = BD\)
-
D.
\(OB = AC\)
Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
-
A.
0, 1, 2, 3
-
B.
0, 2, 4, 6, 8
-
C.
1, 3, 5, 7, 9
-
D.
0 hoặc 5
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
Tính 1 454-997
-
A.
575
-
B.
567
-
C.
457
-
D.
754
Cho hình thang có độ dài hai cạnh bên là 5 cm và 7 cm, đáy lớn gấp đôi đáy nhỏ, biết độ dài đáy nhỏ là 6 cm. Chu vi hình thang là:
-
A.
36 cm
-
B.
18 cm
-
C.
30 cm
-
D.
24 cm
Tổng \(1 + 2 + 3 + 4 + ... + 2018\) bằng
-
A.
\(4074342\)
-
B.
\(2037171\)
-
C.
\(2036162\)
-
D.
\(2035152\)
Tìm số tự nhiên \(n\) biết \({3^n} = 81.\)
-
A.
\(n = 2\)
-
B.
\(n = 4\)
-
C.
\(n = 5\)
-
D.
\(n = 8\)
Cho hình vuông ABCD có chu vi bằng 28cm. Diện tích hình vuông ABCD là:
-
A.
\(49\,cm\)
-
B.
\(28\,c{m^2}\)
-
C.
\(49\,c{m^2}\)
-
D.
\(112\,c{m^2}\)
Thay dấu * để được số nguyên tố $\overline {*1} $:
-
A.
$2$
-
B.
$8$
-
C.
$5$
-
D.
$4$
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Trong các số $333; 354; 360; 2457; 1617; 152,$ các số chia hết cho $9$ là
-
A.
$333$
-
B.
$360$
-
C.
$2457$
-
D.
Cả A, B, C đều đúng
Hệ Mặt Trời gồm có Mặt Trời ở trung tâm và 8 thiên thể quanh quanh Mặt Trời gọi là các hành tinh. Đó là sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương.
Cho S là tập hợp các hành tinh của Hệ Mặt Trời. Khẳng định nào sau đây đúng ?
-
A.
S là tập hợp có 8 phần tử.
-
B.
Sao Thủy không thuộc S.
-
C.
S là tập hợp có 9 phần tử.
-
D.
Mặt Trời là một phần tử của S.
Phân tích số \(a\) ra thừa số nguyên tố \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\), khẳng định nào sau đây là đúng:
-
A.
Các số \({p_1};\,{p_2};...;\,{p_k}\) là các số dương.
-
B.
Các số \({p_1};\,{p_2};...;\,{p_k} \in P\)(với $P$ là tập hợp các số nguyên tố).
-
C.
Các số \({p_1};\,{p_2};...;\,{p_k} \in N\).
-
D.
Các số \({p_1};\,{p_2};...;\,{p_k}\) tùy ý.
\(\overline {a001} \left( {a \ne 0} \right)\) bằng
-
A.
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\)
-
B.
\(\overline {a001} = 1000 + 0 \times 100 + 0 \times 10 + 1\)
-
C.
\(\overline {a001} = a \times 1000 + 1 \times 100\)
-
D.
\(\overline {a001} = a + 0 + 0 + 1\)
Có bao nhiêu số vừa là bội của $5$ vừa là ước của $50$?
-
A.
$4$ số
-
B.
$5$ số
-
C.
$6$ số
-
D.
$7$ số
Tìm số tự nhiên \(\overline {145*} \) chia hết cho cả \(3\) và \(5.\)
-
A.
\(1454\)
-
B.
\(1450\)
-
C.
\(1455\)
-
D.
\(1452\)
Nếu cho 7 hình vuông đơn vị ghép thành hình chữ nhật thì có mấy cách xếp (Không kể việc xoay chiều dài và chiều rộng)?
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Tìm tất cả các số tự nhiên \(n\) để \({n^2} + 12n\) là số nguyên tố.
-
A.
$n = 11$
-
B.
$n = 13$
-
C.
$n = 2$
-
D.
$n = 1$
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ \(800\) đến \(900\) em.
-
A.
$845$
-
B.
$840$
-
C.
$860$
-
D.
$900$
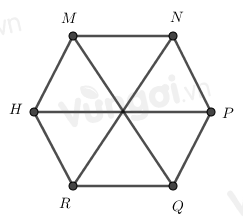
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
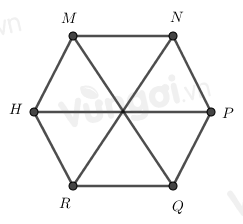
-
A.
8
-
B.
2
-
C.
4
-
D.
6
Diện tích của một hình chữ nhật có chiều rộng 26 cm và có chu vi gấp 3 lần chiều dài là:
-
A.
\(2028\,\,cm\)
-
B.
\(1352\,\,cm\)
-
C.
\(2028\,\,c{m^2}\)
-
D.
\(1352\,\,c{m^2}\)
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Tìm hai số tự nhiên $a,b\left( {a < b} \right).$ Biết $a + b = 20,BCNN\left( {a,b} \right) = 15.$
-
A.
$a = 15;b = 25.$
-
B.
$a = 15;b = 5.$
-
C.
$a = 15;b = 20.$
-
D.
$a = 5;b = 15.$
Toán vui. Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí nhìn khác nhau nên hai bạn thấy hai dãy các phép tính khác nhau.

Phép tính Toàn quan sát được để phép tính hai bạn quan sát thấy bằng nhau là:
-
A.
\({\bf{11}} + {\bf{8}}1 + 1{\bf{9}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{270}} \)
-
B.
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{275}} \)
-
C.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
-
D.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{6}}8 + {\bf{9}}1 + 11{\rm{ }} = {\bf{344}} \)
Sân trường em hình vuông. Để tăng thêm diện tích nhà trường mở rộng về mỗi phía 4m thì diện tích tăng thêm 192m 2 . Hỏi trước đây sân trường em có diện tích là bao nhiêu m 2 ?
-
A.
16 m 2
-
B.
32 m 2
-
C.
64 m 2
-
D.
128 m 2
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
-
A.
Hai số trên có hai ước chung
-
B.
Hai số trên có ba ước chung
-
C.
Hai số trên là hai số nguyên tố cùng nhau
-
D.
Hai số trên chỉ có một ước chung là 3.
Lời giải và đáp án
Chọn câu đúng:
-
A.
Diện tích hình bình hành bằng nửa tích của cạnh đáy nhân với chiều cao.
-
B.
Diện tích hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Diện tích hình bình hành bằng hiệu của cạnh đáy và chiều cao.
Đáp án : C
Diện tích hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
Tìm tập hợp các bội của $6$ trong các số: $6;15;24;30;40$.
-
A.
$\left\{ {15;24} \right\}$
-
B.
$\left\{ {24;30} \right\}$
-
C.
$\left\{ {15;24;30} \right\}$
-
D.
$\left\{ {6;24;30} \right\}$
Đáp án : D
\(B\left( 6 \right) = \left\{ {6.m|m \in N} \right\}\)
Trong các số trên thì $B\left( 6 \right) = \left\{ {6;24;30} \right\}$
Tìm số tự nhiên $x$ thỏa mãn: $7+x=362$.
-
A.
300
-
B.
355
-
C.
305
-
D.
362
Đáp án : B
Tìm số hạng chưa biết: Lấy tổng trừ đi số hạng đã biết.
Ta có:
$7+x=362$
$x=362-7$
$x=355$.
Tìm $x$ biết: \(65 - {4^{x + 2}} = 1\)
-
A.
$5$
-
B.
$4$
-
C.
$3$
-
D.
$1$
Đáp án : D
Nhận thấy $65$ là số bị trừ; ${4^{x + 2}}$ là số trừ và $1$ là hiệu nên muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
Từ đó biến đổi về dạng hai lũy thừa cùng cơ số rồi cho hai số mũ bằng nhau.
\(\begin{array}{l}65 - {4^{x + 2}} = 1\\\,\,\,\,\,\,\,\,\,\,\,{4^{x + 2}}\,\, = 65 - 1\\\,\,\,\,\,\,\,\,\,\,{4^{x + 2}}\,\,\, = 64\\\,\,\,\,\,\,\,\,\,\,{4^{x + 2}}\,\,\, = {4^3}\\\,\,\,\,\,\,\;\;\,x + 2\,= 3\\\,\,\,\,\,\,\,\;\;x\,\,\,\,\,\,\,\,\,\,\,= 3 - 2\\\,\,\,\;\;\,\,\,x\,\,\,\,\,\,\,\,\,\,\,\, = 1\end{array}\)
-
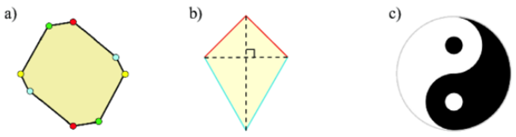
A.
Hình a
-
B.
Hình b
-
C.
Hình c
-
D.
Hình a và Hình c
Đáp án : A
Hình a có tâm đối xứng:
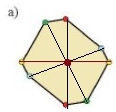
Tập hợp số tự nhiên được kí hiệu là
-
A.
\(N\)
-
B.
\({N^*}\)
-
C.
\(\left\{ N \right\}\)
-
D.
\(Z\)
Đáp án : A
Tập hợp số tự nhiên kí hiệu là N.
\({7^2}{.7^4}:{7^3}\) bằng
-
A.
\({7^1}\)
-
B.
\({7^2}\)
-
C.
\({7^3}\)
-
D.
\({7^9}\)
Đáp án : C
Lấy \({7^2}{.7^4}\) rồi chia cho \({7^3}\)
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.
\({a^m}:{a^n} = {a^{m - n}}\) \(\left( {a \ne 0;\,m \ge n \ge 0} \right)\)
\(\begin{array}{l}{7^2}{.7^4} = {7^{2 + 4}} = {7^6}\\{7^2}{.7^4}:{7^3} = {7^6}:{7^3} = {7^{6 - 3}} = {7^3}\end{array}\)
Khi phân tích 104 thành tích các thừa số nguyên tố thì số mũ của thừa số 2 là
-
A.
2
-
B.
1
-
C.
3
-
D.
4
Đáp án : C
$104=2.2.2.13=2^3.13$
Vậy số mũ của thừa số 2 là 3.
Giá trị của biểu thức \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\) bằng
-
A.
$140$
-
B.
$60$
-
C.
$80$
-
D.
$40$
Đáp án : D
Thực hiện phép tính trong ngoặc tròn rồi đến ngoặc vuông. Sau đó là phép nhân và phép trừ.
Ta có \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\)
\( = 2\left[ {\left( {195 + 5} \right):8 + 195} \right] - 400\)
\( = 2\left[ {200:8 + 195} \right] - 400\)
\( = 2\left( {25 + 195} \right) - 400\)
\( = 2.220 - 400\)
\( = 440 - 400\)
\( = 40\)
-
A.
\(MQ = NR\)
-
B.
\(MH = RQ\)
-
C.
\(MN = HR\)
-
D.
\(MH = MQ\)
Đáp án : D
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Hình lục giác đều MNPQRH có 3 đường chéo chính bằng nhau nên: \(MQ = NR\)
=> A đúng
Hình lục giác đều MNPQRH có 6 cạnh bằng nhau nên \(MH = RQ\) và \(MN = HR\)
=> B, C đúng.
Do MH là cạnh, MQ là đường chéo chính nên hai đoạn này không bằng nhau
=> D sai
Số $x$ là ước chung của số $a$ và số $b$ nếu:
-
A.
$x \in $Ư$\left( a \right)$ và $x \in B(b)$
-
B.
$x \subset Ư(a)$và $x \subset Ư(b)$
-
C.
$x \in $Ư\(\left( a \right)\) và $x \in $Ư\(\left( b \right)\)
-
D.
$x \notin Ư(a)$ và $x \notin Ư(b)$
Đáp án : C
- Sử dụng kiến ước chung của $2$ số: ước chung của $2$ hay nhiều số là ước của tất cả các số đó.
Số \(x\) là ước chung của \(a,b\) nếu \(x\) vừa là ước của \(a\) vừa là ước của \(b\).
-
A.
Hình con sao biển có trục đối xứng
-
B.
Hình chiếc lá có trục đối xứng
-
C.
Hai hình đều có trục đối xứng.
-
D.
Không có hình nào có trục đối xứng
Đáp án : A

Vậy hình con sao biển có trục đối xứng.
Thay dấu * để được số nguyên tố $\overline {3*} $:
-
A.
$7$
-
B.
$4$
-
C.
$6$
-
D.
$9$
Đáp án : A
- Dấu * có thể nhận các giá trị ${\rm{\{ 7; 4; 6; 9\} }}$
- Dùng định nghĩa số nguyên tố để tìm ra số nguyên tố.
Đáp án A: Vì $37$ chỉ chia hết cho \(1\) và \(37\) nên \(37\) là số nguyên tố, do đó chọn A.
Đáp án B: $34$ không phải là số nguyên tố ($34$ chia hết cho $\left\{ {2;{\rm{ }}4;{\rm{ }} \ldots } \right\}$). Do đó loại B.
Đáp án C: $36$ không phải là số nguyên tố ($36$ chia hết cho $\left\{ {1;\,\,2;{\rm{ 3;}}\,...;\,{\rm{36}}} \right\}$). Do đó loại C.
Đáp án D: $39$ không phải là số nguyên tố ($39$ chia hết cho $\left\{ {1;\,\,3;...\,;\,39} \right\}).$ Do đó loại D.
Trong những số sau, có bao nhiêu số chia hết cho 5?
10005459, 12345, 1254360, 1234544, 155498
-
A.
2
-
B.
3
-
C.
4
-
D.
5
Đáp án : A
Các số có chữ số tận cùng là \(0\) hoặc \(5\) thì chia hết cho \(5\) và chỉ những số đó mới chia hết cho \(5\) .
Số 12345 có chữ số tận cùng là 5 nên chia hết cho 5
Số 1254360 có chữ số tận cùng là 0 nên chia hết cho 5
Các số còn lại không có chữ số tận cùng là 0 cùng không có chữ số tận cùng là 5 nên không chia hết cho 5.
Vậy có 2 số chia hết cho 5.
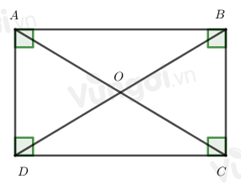
-
A.
\(AB = AC\)
-
B.
\(AC = DO\)
-
C.
\(AC = BD\)
-
D.
\(OB = AC\)
Đáp án : C
Trong hình chữ nhật hai đường chéo bằng nhau
Trong hình chữ nhật hai đường chéo bằng nhau nên \(AC = BD\) => Đáp án C đúng
Đáp án A sai do AB là cạnh, AC là đường chéo nên chúng không bằng nhau.
Đáp án B sai do AC là đường chéo, DO là một nửa đường chéo còn lại nên chúng không bằng nhau.
Đáp án D sai do OB là một nửa đường chéo, AC là đường chéo còn lại nên chúng không bằng nhau.
Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
-
A.
0, 1, 2, 3
-
B.
0, 2, 4, 6, 8
-
C.
1, 3, 5, 7, 9
-
D.
0 hoặc 5
Đáp án : D
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
Đáp án : A
- Áp dụng kiến thức:
Mọi số tự nhiên đều có ước là $1$.
Số nguyên tố có $2$ ước là $1$ và chính nó.
Mọi số nguyên tố khác nhau đều có ước chung duy nhất là $1$.
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$.
B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.
C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.
D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.
Tính 1 454-997
-
A.
575
-
B.
567
-
C.
457
-
D.
754
Đáp án : C
- Thêm vào số bị trừ và số trừ cùng một số sao cho số trừ mới là số tròn chục, tròn trăm, tròn nghìn.
- Tính: (số bị trừ mới) – (số trừ mới).
1 454-997 = (1 454+3)-(997+3)
= 1 457-1 000=457
Cho hình thang có độ dài hai cạnh bên là 5 cm và 7 cm, đáy lớn gấp đôi đáy nhỏ, biết độ dài đáy nhỏ là 6 cm. Chu vi hình thang là:
-
A.
36 cm
-
B.
18 cm
-
C.
30 cm
-
D.
24 cm
Đáp án : C
- Tính độ dài đáy lớn.
- Chu vi của hình thang bằng tổng độ dài các cạnh của hình thang đó.
Độ dài đáy lớn là: \(6.2 = 12\) (cm)
Chu vi hình thang là: \(5 + 7 + 6 + 12 = 30\) (cm)
Tổng \(1 + 2 + 3 + 4 + ... + 2018\) bằng
-
A.
\(4074342\)
-
B.
\(2037171\)
-
C.
\(2036162\)
-
D.
\(2035152\)
Đáp án : B
+ Tính số các số tự nhiên liên tiếp từ \(1\) đến \(2018\) bằng công thức (số cuối-số đầu)+1
+ Tổng các số tự nhiên liên tiếp từ \(1\) đến \(2018\) được tính bằng công thức
(số cuối+số đầu). số các số hạng :2
Số các số tự nhiên liên tiếp từ \(1\) đến \(2018\) là \(2018 - 1 + 1 = 2018\) số
Như vậy từ \(1\) đến \(2018\) có số các số hạng là $2018.$
Tổng \(1 + 2 + 3 + 4 + ... + 2018\)\( = \left( {2018 + 1} \right).2018:2 = 2037171.\)
Tìm số tự nhiên \(n\) biết \({3^n} = 81.\)
-
A.
\(n = 2\)
-
B.
\(n = 4\)
-
C.
\(n = 5\)
-
D.
\(n = 8\)
Đáp án : B
Đưa hai vế về hai lũy thừa cùng số mũ rồi sử dụng \({a^n} = {a^m}\left( {a \ne 0;a \ne 1} \right)\) thì \(n = m.\)
Ta có \({3^n} = 81\) mà \(81 = {3^4}\) nên \({3^n} = {3^4}\) suy ra \(n = 4.\)
Cho hình vuông ABCD có chu vi bằng 28cm. Diện tích hình vuông ABCD là:
-
A.
\(49\,cm\)
-
B.
\(28\,c{m^2}\)
-
C.
\(49\,c{m^2}\)
-
D.
\(112\,c{m^2}\)
Đáp án : C
- Cạnh của hình vuông = Chu vi : 4
=> Diện tích hình vuông.
- Ta có cạnh AB = BC = CD = DA = 28 : 4 = 7 cm. - Diện tích hình vuông ABCD = 7 .7 = 49 cm 2 .
Thay dấu * để được số nguyên tố $\overline {*1} $:
-
A.
$2$
-
B.
$8$
-
C.
$5$
-
D.
$4$
Đáp án : D
+ Dấu * có thể nhận các giá trị \(\left\{ {2;8;5;4} \right\}\)
+ Dùng định nghĩa số nguyên tố để tìm ra số nguyên tố
Dấu * có thể nhận các giá trị \(\left\{ {2;8;5;4} \right\}\)
+) Ta có \(21\) có các ước \(1;3;7;21\) nên \(21\) là hợp số. Loại A
+) \(81\) có các ước \(1;3;9;27;81\) nên \(81\) là hợp số. Loại B
+) \(51\) có các ước \(1;3;17;51\) nên \(51\) là hợp số. Loại C
+) \(41\) chỉ có hai ước là \(1;41\) nên \(41\) là số nguyên tố.
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : C
Đặt tính rồi tính.
Đếm số các phép chia có dư.
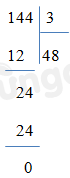

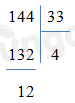

Vậy có 3 phép chia có dư
Trong các số $333; 354; 360; 2457; 1617; 152,$ các số chia hết cho $9$ là
-
A.
$333$
-
B.
$360$
-
C.
$2457$
-
D.
Cả A, B, C đều đúng
Đáp án : D
Sử dụng dấu hiệu chia hết cho $9$ : Các số có tổng các chữ số chia hết cho $9$ thì chia hết cho $9.$
Các số $333;2457;360$ là các số chia hết cho $9$ vì tổng các chữ số của nó chia hết cho $9.$
+) Số $333$ có tổng các chữ số là $3+3+3=9 \, \vdots \, 9$ nên $ 333 \, \vdots \, 9.$
+) Số $2457$ có tổng các chữ số là $2+4+5+7=18 \, \vdots \, 9$ nên $ 2457 \, \vdots \, 9.$
+) Số $360$ có tổng các chữ số là $3+6+0=9 \, \vdots \, 9$ nên $ 360 \, \vdots \, 9.$
Các số còn lại $354; 1617; 152$ đều có tổng các chữ số không chia hết cho $9$ nên chúng không chia hết cho $9$.
Hệ Mặt Trời gồm có Mặt Trời ở trung tâm và 8 thiên thể quanh quanh Mặt Trời gọi là các hành tinh. Đó là sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương.
Cho S là tập hợp các hành tinh của Hệ Mặt Trời. Khẳng định nào sau đây đúng ?
-
A.
S là tập hợp có 8 phần tử.
-
B.
Sao Thủy không thuộc S.
-
C.
S là tập hợp có 9 phần tử.
-
D.
Mặt Trời là một phần tử của S.
Đáp án : A
+) Các hành tinh của Hệ Mặt Trời là sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương.
+) Mỗi một hành tinh là một phần tử của tập hợp.
+) Số hành tinh là số phần tử của S.
Thổ, Sao Thiên Vương, Sao Hải Vương
Hệ Mặt Trời có 8 hành tinh nên S có 8 phần tử => A đúng, C sai
Sao Thủy là một hành tinh của Hệ Mặt Trời => B sai.
Mặt Trời không là hành tinh nên Mặt Trời không là một phần tử của S => D sai
Phân tích số \(a\) ra thừa số nguyên tố \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\), khẳng định nào sau đây là đúng:
-
A.
Các số \({p_1};\,{p_2};...;\,{p_k}\) là các số dương.
-
B.
Các số \({p_1};\,{p_2};...;\,{p_k} \in P\)(với $P$ là tập hợp các số nguyên tố).
-
C.
Các số \({p_1};\,{p_2};...;\,{p_k} \in N\).
-
D.
Các số \({p_1};\,{p_2};...;\,{p_k}\) tùy ý.
Đáp án : B
- Áp dụng kiến thức về phân tích $1$ số thành thừa số nguyên tố (các thừa số trong tích phải là số nguyên tố)
Khi phân tích một số \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\) ra thừa số nguyên tố thì các số \({p_1},{p_2},...,{p_k}\) phải là các số nguyên tố.
\(\overline {a001} \left( {a \ne 0} \right)\) bằng
-
A.
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\)
-
B.
\(\overline {a001} = 1000 + 0 \times 100 + 0 \times 10 + 1\)
-
C.
\(\overline {a001} = a \times 1000 + 1 \times 100\)
-
D.
\(\overline {a001} = a + 0 + 0 + 1\)
Đáp án : A
- Xác định hàng của từng chữ số trong mỗi số.
- Chữ số hàng đơn vị ta giữ nguyên
- Chữ số hàng chục nhân với 10.
- Chữ số hàng trăm nhân với 100.
- Chữ số hàng nghìn nhân với 1000.
Số a là chữ số hàng nghìn nên ta nhân với 1000.
Hai số 0 lần lượt là hàng trăm (nhân với 100) và hàng chục (nhân với 10).
Số 1 là chữ số hàng đơn vị (nhân với 1).
\(\overline {a001} = a \times 1000 + 0 \times 100 + 0 \times 10 + 1\).
Có bao nhiêu số vừa là bội của $5$ vừa là ước của $50$?
-
A.
$4$ số
-
B.
$5$ số
-
C.
$6$ số
-
D.
$7$ số
Đáp án : A
$\,\left\{ \begin{array}{l}B\left( 5 \right) = {\rm{\{ 5}}{\rm{.k| k}} \in {\rm{N\} }}\\Ư(50) = {\rm{\{ x}} \in {\rm{N}}|50 \, \vdots \, x{\rm{\} }}\end{array} \right.$
Gọi $x$ là số vừa là bội của $5$ vừa là ước của $50$.
\(\left\{ \begin{array}{l}x \in B\left( 5 \right)\\x \in Ư\left( {50} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x \in {\rm{\{ 0;}}\,{\rm{5;10;15;20;25;}}...{\rm{\} }}\\x \in {\rm{\{ 1;2;5;10;25;50\} }}\end{array} \right.\)
\( \Rightarrow \,x\, \in \,{\rm{\{ 5;10;25;50\} }}\)
Tìm số tự nhiên \(\overline {145*} \) chia hết cho cả \(3\) và \(5.\)
-
A.
\(1454\)
-
B.
\(1450\)
-
C.
\(1455\)
-
D.
\(1452\)
Đáp án : C
+ Các số chia hết cho \(5\) có chữ số tận cùng là \(0\) hoặc \(5.\)
+ Các số chia hết cho \(3\) có tổng các chữ số chia hết cho \(3.\)
Từ đó lập luận để tìm các số thỏa mãn.
Vì \(\overline {145*} \) chia hết cho \(5\) nên \(*\) có thể bằng \(0\) hoặc \(5.\)
+ Nếu \(*\) bằng \(0\) thì ta được số \(1450\) có \(1 + 4 + 5 + 0 = 10\not \vdots 3\) nên loại
+ Nếu \(*\) bằng \(5\) thì ta được số \(1455\) có \(1 + 4 + 5 + 5 = 15 \vdots 3\) nên thỏa mãn.
Vậy số cần tìm là \(1455.\)
Nếu cho 7 hình vuông đơn vị ghép thành hình chữ nhật thì có mấy cách xếp (Không kể việc xoay chiều dài và chiều rộng)?
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : A
Hình vuông đơn vị là hình vuông có cạnh bằng 1.
Để xếp các hình vuông đơn vị thành hình chữ nhật thì số lượng hình vuông phải chia hết cho độ dài các cạnh của hình chữ nhật.
Nếu xếp 7 hình vuông đơn vị thành hình chữ nhật thì chiều rộng của hình chữ nhật chỉ có thể xếp:

Tìm tất cả các số tự nhiên \(n\) để \({n^2} + 12n\) là số nguyên tố.
-
A.
$n = 11$
-
B.
$n = 13$
-
C.
$n = 2$
-
D.
$n = 1$
Đáp án : D
+ Phân tích \({n^2} + 12n = n\left( {n + 12} \right)\)
+ Dựa vào định nghĩa số nguyên tố để lập luận và suy ra các giá trị của \(n.\)
Ta có \({n^2} + 12n = n\left( {n + 12} \right);\,n + 12 > 1\) nên để \({n^2} + 12n\) là số nguyên tố thì \(n = 1.\)
Thử lại \({n^2} + 12n = {1^2} + 12.1 = 13\) (nguyên tố)
Vậy với \(n = 1\) thì \({n^2} + 12n\) là số nguyên tố.
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ \(800\) đến \(900\) em.
-
A.
$845$
-
B.
$840$
-
C.
$860$
-
D.
$900$
Đáp án : A
+ Sử dụng kiến thức về phép chia có dư.
+ Sử dụng kiến thức về bội chung và bội chung nhỏ nhất.
+ Sử dụng cách tìm bội chung thông qua bội chung nhỏ nhất.
Gọi số học sinh đi thăm quan là \(x\,\left( {x \in {N^*};\,800 \le x \le 900} \right)\) (học sinh)
Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi nghĩa là thừa ra 5 học sinh nên ta có
\(\left( {x - 5} \right) \vdots 35;\,\left( {x - 5} \right) \vdots 40\) suy ra \(\left( {x - 5} \right) \in BC\left( {35;40} \right)\).
Ta có \(35 = 5.7;\,40 = {2^3}.5\) nên \(BCNN\left( {35;40} \right) = {2^3}.5.7 = 280.\)
Suy ra \((x-5) \in BC\left( {35;40} \right) = B\left( {280} \right) = \left\{ {280;560;840;1120;...} \right\}\) mà \(800 \le x \le 900\) nên \(x -5= 840\) hay $x=845.$
Vậy số học sinh đi thăm quan là \(845\) học sinh.
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

-
A.
8
-
B.
2
-
C.
4
-
D.
6
Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
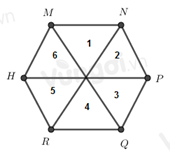
Ta đánh số như hình trên
Nhận thấy có các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.
Diện tích của một hình chữ nhật có chiều rộng 26 cm và có chu vi gấp 3 lần chiều dài là:
-
A.
\(2028\,\,cm\)
-
B.
\(1352\,\,cm\)
-
C.
\(2028\,\,c{m^2}\)
-
D.
\(1352\,\,c{m^2}\)
Đáp án : D
Chu vi = 3. chiều dài
=> Chu vi = 2. chiều dài + chiều dài.
Mà: Chu vi = 2. chiều dài + 2. chiều rộng
=> Chiều dài = 2.chiều rộng.
Từ đó tìm được chiều dài và tính được diện tích của hình chữ nhật.
Theo đề bài:
Chu vi = 3. chiều dài
=> Chu vi = 2. chiều dài + chiều dài.
Mà: Chu vi = 2. chiều dài + 2. chiều rộng
=> Chiều dài = 2. chiều rộng.
Suy ra chiều dài hình chữ nhật là: 2. 26 = 52 cm.
Diện tích hình chữ nhật là: 52 . 26 = 1352 (cm 2 ).
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : C
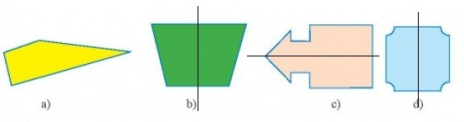
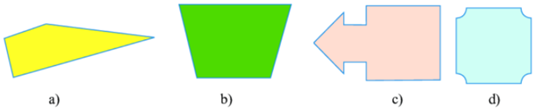
=> Các hình có trục đối xứng là: b, c, d.
Vậy có 3 hình có trục đối xứng.
Tìm hai số tự nhiên $a,b\left( {a < b} \right).$ Biết $a + b = 20,BCNN\left( {a,b} \right) = 15.$
-
A.
$a = 15;b = 25.$
-
B.
$a = 15;b = 5.$
-
C.
$a = 15;b = 20.$
-
D.
$a = 5;b = 15.$
Đáp án : D
Gọi ƯCLN$\left( {a,b} \right) = d$ Tìm $d \in $ ƯC$\left( {15;20} \right)$ sau đó thay $d$ vào công thức $a.b = $ƯCLN$\left( {a,b} \right).BCNN\left( {a,b} \right),$ kết hợp điều kiện $a + b = 20$ để tìm $a$ và $b$.
Gọi ƯCLN$\left( {a,b} \right) = d$ $ \Rightarrow a = d.m,b = d.n;\left( {m,n} \right) = 1$ $ \Rightarrow a + b = d\left( {m + n} \right)$ $ \Rightarrow d \in $ Ư$\left( {a + b} \right)$ hay $d \in $Ư$\left( {20} \right)$ Vì $BCNN\left( {a,b} \right) = 15$ \( \Rightarrow 15 \vdots d\) hay $d \in $Ư$\left( {15} \right)$ $ \Rightarrow d \in $ ƯC$\left( {15;20} \right)$ Mà ƯCLN$\left( {15;20} \right) = 5$ nên $d = 1$ hoặc $d = 5$ +) Nếu $d = 1 \Rightarrow a.b = 1.15 = 15 = 3.5$ Khi đó $a + b = 3 + 5 = 8$ (loại) Hoặc $a + b = 1 + 15 = 16$ (loại) +) Nếu $d = 5$ thì $a.b = 5.15 = 75 = 1.75$ Khi đó $a + b = 15 + 5 = 20$ (thỏa mãn) Hoặc $a + b = 1 + 75 = 76$ (loại) Vậy hai số cần tìm là $a = 5;b = 15.$
Toán vui. Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí nhìn khác nhau nên hai bạn thấy hai dãy các phép tính khác nhau.

Phép tính Toàn quan sát được để phép tính hai bạn quan sát thấy bằng nhau là:
-
A.
\({\bf{11}} + {\bf{8}}1 + 1{\bf{9}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{270}} \)
-
B.
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{275}} \)
-
C.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
-
D.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{6}}8 + {\bf{9}}1 + 11{\rm{ }} = {\bf{344}} \)
Đáp án : C
Điền các số: 1; 6; 8; 9 vào ô trống để được phép tính đúng.
Phép tính Toàn quan sát được là:
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
Phép tính Na quan sát được là:
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{69}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{344}} \)
Sân trường em hình vuông. Để tăng thêm diện tích nhà trường mở rộng về mỗi phía 4m thì diện tích tăng thêm 192m 2 . Hỏi trước đây sân trường em có diện tích là bao nhiêu m 2 ?
-
A.
16 m 2
-
B.
32 m 2
-
C.
64 m 2
-
D.
128 m 2
Đáp án : C
- Diện tích tăng thêm bằng diện tích 4 hình vuông nhỏ cạnh bằng 4m và 4 hình chữ nhật có 1 cạnh bằng 4 m và 1 cạnh bằng cạnh hình vuông
- Tinh diện tích 4 hình vuông nhỏ
- Tính diện tích 4 hình chữ nhật
- Tính diện tích 1 hình chữ nhật
- Tính cạnh hình vuông đã cho
=> Diện tích sân trường lúc chưa mở rộng.
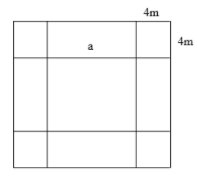
Diện tích tăng thêm bằng diện tích 4 hình vuông nhỏ cạnh bằng 4m và 4 hình chữ nhật có 1 cạnh bằng 4 m và 1 cạnh bằng cạnh hình vuông
Diện tích 4 hình vuông nhỏ là: 4 . (4 . 4) = 64 m 2
Diện tích 4 hình chữ nhật là: 192 - 64 = 128 m 2
Diện tích 1 hình chữ nhật là 128 : 4 = 32 m 2
Cạnh hình vuông đã cho là: 32 : 4 = 8 m
Diện tích sân trường lúc chưa mở rộng là: 8 . 8 = 64 m 2
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
-
A.
Hai số trên có hai ước chung
-
B.
Hai số trên có ba ước chung
-
C.
Hai số trên là hai số nguyên tố cùng nhau
-
D.
Hai số trên chỉ có một ước chung là 3.
Đáp án : C
Dựa vào kiến thức 2 số nguyên tố cùng nhau là 2 số nguyên tố có ước chung lớn nhất là 1.
Áp dụng tính chất chia hết của 1 hiệu: Nếu $a \vdots c;b \vdots c \Rightarrow \left( {a - b} \right) \vdots c$
Gọi \(d = UCLN\left( {14n + 3;21n + 4} \right)\) ta có:
\(14n + 3\, \vdots \,d\) và \(21n + 4 \, \vdots \, d\)
\(3\left( {14n + 3} \right) \vdots \, d\) và \(2\left( {21n + 4} \right) \vdots d\)
\(42n + 9 \,\vdots \, d\) và \(42n + 8 \, \vdots \, d\)
\(\left( {42n + 9} \right) - \left( {42n + 8} \right) \vdots d\)
Suy ra \(1 \vdots d\)
\(d = 1\)
Vậy \(ƯCLN\left( {14n + 3;21n + 4} \right) = 1\) hay hai số đó là hai số nguyên tố cùng nhau.