Đề kiểm tra học kì 1 Toán 6 Cánh diều - Đề số 1
Đề bài
Cách viết tập hợp nào sau đây là đúng?
-
A.
\(A = \left[ {0;1;2;3} \right]\)
-
B.
\(A = \left( {0;1;2;3} \right)\)
-
C.
\(A = 1;2;3\)
-
D.
\(A = \left\{ {0;1;2;3} \right\}\)
Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
-
A.
0, 1, 2, 3
-
B.
0, 2, 4, 6, 8
-
C.
1, 3, 5, 7, 9
-
D.
0 hoặc 5
Thu gọn biểu thức \(z - (x + y - z) - \left( { - x} \right)\) ta được:
-
A.
\(2y - x\)
-
B.
\(y - 2x\)
-
C.
\(2z - y\)
-
D.
\(y\)
Khẳng định nào là sai:
-
A.
$0$ và $1$ không là số nguyên tố cũng không phải hợp số.
-
B.
Cho số $a > 1$, $a$ có $2$ ước thì $a$ là hợp số.
-
C.
$2$ là số nguyên tố chẵn duy nhất.
-
D.
Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó.
-
A.
\(AB = 2\,\,cm\)
-
B.
\(AD = 8\,\,cm\)
-
C.
\(DC = 4\,\,cm\)
-
D.
\(AB = 8\,\,cm\)
Chọn câu đúng.
-
A.
\(\left( { - 20} \right).\left( { - 5} \right) = - 100\)
-
B.
\(\left( { - 50} \right).\left( { - 12} \right) = 600\)
-
C.
\(\left( { - 18} \right).25 = - 400\)
-
D.
\(11.\left( { - 11} \right) = - 1111\)
Cho n là một số tự nhiên lớn hơn 2 và nhỏ hơn 5. Khẳng định nào sau đây đúng ?
-
A.
n nằm bên phải điểm 5 trên tia số
-
B.
n nằm bên trái điểm 2 trên tia số
-
C.
n nằm bên phải điểm 2 trên tia số
-
D.
n nằm bên phải điểm 5 và cách điểm 5 một đơn vị trên tia số.
Hình lục giác đều có mấy cạnh
-
A.
3
-
B.
5
-
C.
6
-
D.
8
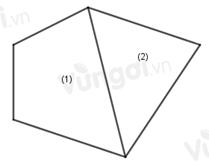
Cho diện tích tứ giác (1) bằng \(20\,\,c{m^2}\), Diện tích tam giác (2) bằng \(16\,\,c{m^2}\), Khi đó diện tích của hình trên bằng:
-
A.
\(36\,cm\)
-
B.
\(36\,d{m^2}\)
-
C.
\(26\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
Cho bảng số liệu về các loại quả ưa thích của các bạn trong lớp 6A2 như sau
|
Các loại quả |
Cam |
Xoài |
Chuối |
Khế |
Ổi |
|
Số bạn thích |
8 |
9 |
6 |
4 |
3 |
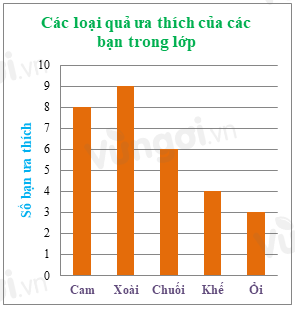
Điền số mấy ở trên cột Khế?
-
A.
9
-
B.
8
-
C.
6
-
D.
4
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Điểm thi của Nam và Khải được biểu diễn trong biểu đồ cột kép ở hình sau:
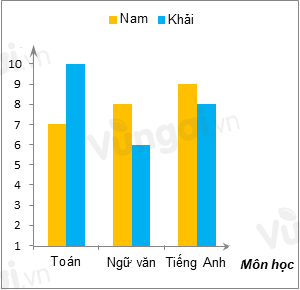
Khẳng định nào sau đây đúng ?
-
A.
Điểm Toán của Nam cao hơn Khải
-
B.
Điểm cả 3 môn của Khải cao hơn Nam
-
C.
Điểm Ngữ văn của Nam cao hơn Khải
-
D.
Điểm Ngữ văn của Khải cao hơn Nam
Hình thang cân có:
-
A.
1 cạnh bên
-
B.
2 cạnh bên
-
C.
3 cạnh bên
-
D.
4 cạnh bên

Điền số thích hợp vào chỗ trống:
Kiểm tra thị lực của một học sinh trường THCS, ta thu được bảng kết quả như sau:
|
Khối |
Số học sinh được kiểm tra |
Số học sinh bị tật khúc xạ (cận thị, viễn thị, loạn thị) |
|
6 |
210 |
14 |
|
7 |
200 |
30 |
|
8 |
180 |
40 |
|
9 |
170 |
51 |
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
Tìm $x$ biết: $44 - x - 16{\rm{ }} = - 60$
-
A.
\(x = - 88\)
-
B.
\(x = - 42\)
-
C.
\(x = 42\)
-
D.
\(x = 88\)
\(5125 + 456875\) bằng
-
A.
\(46200\)
-
B.
\(462000\)
-
C.
\(46300\)
-
D.
\(426000\)
5 là phần tử của
-
A.
Ư\(\left( {14} \right)\)
-
B.
Ư\(\left( {15} \right)\)
-
C.
Ư\(\left( {16} \right)\)
-
D.
Ư\(\left( {17} \right)\)
Lan tìm hiểu về thức ăn sáng nay của các bạn trong lớp và thu được kết quả như sau:

Dữ liệu nào sau đây không là số liệu?
-
A.
Xôi
-
B.
11
-
C.
8
-
D.
2
Tính \(3.\left( {{2^3}.4 - 6.5} \right)\)
-
A.
6
-
B.
3
-
C.
2
-
D.
1
Một cửa hàng bán kính ghi lại số kính bán được trong tháng bằng bảng số liệu sau:
Số kính bán được trong tháng
|
Màu kính |
Trắng |
Đen |
Xanh |
Trắng bạc |
Vàng kim |
|
Số lượng |
20 |
10 |
30 |
15 |
25 |
Sử dụng các biểu tượng sau để vẽ biểu đồ tranh
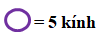
Cần bao nhiêu biểu tượng hình tròn màu tím để biểu diễn số kính màu vàng kim?
-
A.
25
-
B.
4
-
C.
5
-
D.
6
Hình chữ nhật có bao nhiêu trục đối xứng
-
A.
1
-
B.
2
-
C.
3
-
D.
4
-
A.
Tổng của hai số nguyên cùng dấu là một số nguyên âm.
-
B.
Tổng của hai số nguyên âm là một số nguyên âm.
-
C.
Tổng của hai số nguyên cùng dấu là một số nguyên dương.
-
D.
Tổng của hai số nguyên dương là một số nguyên âm.
Tập hợp các kết quả có thể xảy ra của phép thử nghiệm tung một đồng xu là
-
A.
\(X = \left\{ {N,S} \right\}\)
-
B.
\(X = \left\{ N \right\}\)
-
C.
\(X = \left\{ S \right\}\)
-
D.
\(X = \left\{ {NN,S} \right\}\)
Viết tích \({a^4}.{a^6}\) dưới dạng một lũy thừa ta được
-
A.
\({a^8}\)
-
B.
\({a^9}\)
-
C.
\({a^{10}}\)
-
D.
\({a^2}\)
Tập hợp các số nguyên kí hiệu là
-
A.
$N$
-
B.
${N^*}$
-
C.
$Z$
-
D.
${Z^*}$
-
A.
Hình a
-
B.
Hình b
-
C.
Hình c
-
D.
Hình a và Hình c
Kết quả của phép tính \(\left( {158.129 - 158.39} \right):180\) có chữ số tận cùng là
-
A.
\(8\)
-
B.
\(79\)
-
C.
\(9\)
-
D.
\(5\)
Gọi \({x_1}\) là giá trị thỏa mãn \({5^{x - 2}} - {3^2} = {2^4} - \left( {{2^8}{{.2}^4} - {2^{10}}{{.2}^2}} \right)\) và \({x_2}\) là giá trị thỏa mãn \(697:\left[ {\left( {15.x + 364} \right):x} \right] = 17\) . Tính \({x_1}.{x_2}\).
-
A.
$14$
-
B.
$56$
-
C.
$4$
-
D.
$46$
Tìm số tự nhiên \(\overline {145*} \) chia hết cho cả \(3\) và \(5.\)
-
A.
\(1454\)
-
B.
\(1450\)
-
C.
\(1455\)
-
D.
\(1452\)
Một căn phòng hình chữ nhật dài $680$cm, rộng $480$cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch có độ dài lớn nhất là bao nhiêu?
-
A.
$5\,cm$
-
B.
$10\,cm$
-
C.
$20\,cm$
-
D.
$40\,cm$
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ \(800\) đến \(900\) em.
-
A.
$845$
-
B.
$840$
-
C.
$860$
-
D.
$900$
Biết \( - 9 < x < 0\). Tập hợp các số nguyên $x$ thỏa mãn:
-
A.
\(A = \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\)
-
B.
\(A = \left\{ { - 9; - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\)
-
C.
\(A = \left\{ { - 9; - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1;0} \right\}\)
-
D.
\(A = \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1;0} \right\}\)
-
A.
\( - 2021;\,\, - 10;\,\,4;\,0;\, - 1\)
-
B.
\( - 2021;\,\, - 10;\,\, - 1;\,\,0;\,\,4\)
-
C.
\( - 2021;\,\, - 10;\,\,0;\,\, - 1;\,\,4\)
-
D.
\(4;\,0;\, - 1;\, - 10;\, - 2021\)

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\)
B. \(17cm\)
C. \(18cm\)
D. \(19cm\)
-
A.
Tam giác đều
-
B.
Cánh quạt
-
C.
Trái tim
-
D.
Cánh diều
Tìm các giá trị thích hợp của chữ số $a$ sao cho: \( - \overline {a99} > - 649 > - \overline {6a0} \)
-
A.
$6$
-
B.
$5$
-
C.
$4$
-
D.
$7$
Toán vui. Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí nhìn khác nhau nên hai bạn thấy hai dãy các phép tính khác nhau.

Phép tính Toàn quan sát được để phép tính hai bạn quan sát thấy bằng nhau là:
-
A.
\({\bf{11}} + {\bf{8}}1 + 1{\bf{9}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{270}} \)
-
B.
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{275}} \)
-
C.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
-
D.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{6}}8 + {\bf{9}}1 + 11{\rm{ }} = {\bf{344}} \)
Cho phép tính \(\overline {ab} .\,c\, = 424.\) Khi đó \(c\) bằng bao nhiêu?
-
A.
$9$
-
B.
$8$
-
C.
$5$
-
D.
$6$
Chọn câu đúng nhất.
-
A.
\(\left( {a - b} \right) + \left( {c - d} \right) - \left( {a + c} \right) = - \left( {b + d} \right)\)
-
B.
\(\left( {a - b} \right) - \left( {c - d} \right) + \left( {b + c} \right) = a + d\)
-
C.
\(\left( {a - b} \right) - \left( {c - d} \right) + \left( {b - a} \right) = - \left( {c - d} \right)\)
-
D.
Cả A, B, C đều đúng
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
-
A.
\(6\)
-
B.
\(46\)
-
C.
\(16\)
-
D.
\(5\)
Lời giải và đáp án
Cách viết tập hợp nào sau đây là đúng?
-
A.
\(A = \left[ {0;1;2;3} \right]\)
-
B.
\(A = \left( {0;1;2;3} \right)\)
-
C.
\(A = 1;2;3\)
-
D.
\(A = \left\{ {0;1;2;3} \right\}\)
Đáp án : D
Sử dụng cách viết tập hợp
+ Tên tập hợp được viết bằng các chữ cái in hoa như A ; B ; C ;...
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ” (nếu có phần tử số)
Cách viết đúng là \(A = \left\{ {0;1;2;3} \right\}.\)
Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
-
A.
0, 1, 2, 3
-
B.
0, 2, 4, 6, 8
-
C.
1, 3, 5, 7, 9
-
D.
0 hoặc 5
Đáp án : D
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Thu gọn biểu thức \(z - (x + y - z) - \left( { - x} \right)\) ta được:
-
A.
\(2y - x\)
-
B.
\(y - 2x\)
-
C.
\(2z - y\)
-
D.
\(y\)
Đáp án : C
Khi bỏ dấu ngoặc, nếu đằng trước dấu ngoặc:
Có dấu “-”, thì phải đổi dấu tất cả các số hạng trong ngoặc
\( - \left( {a + b - c} \right) = - a - b + c\)
\(\begin{array}{l}z - (x + y - z) - \left( { - x} \right) = z - x - y + z + x\\ = \left( { - x + x} \right) + \left( {z + z} \right) - y\\ = 0 + 2z - y\\ = 2z - y\end{array}\)
Khẳng định nào là sai:
-
A.
$0$ và $1$ không là số nguyên tố cũng không phải hợp số.
-
B.
Cho số $a > 1$, $a$ có $2$ ước thì $a$ là hợp số.
-
C.
$2$ là số nguyên tố chẵn duy nhất.
-
D.
Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó.
Đáp án : B
Áp dụng định nghĩa:
+ Hợp số là một số tự nhiên có thể biểu diễn thành tích của hai số tự nhiên khác nhỏ hơn nó. Một định nghĩa khác tương đương: hợp số là số chia hết cho các số khác ngoài 1 và chính nó.
+ Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó.
+) Số $a$ phải là số tự nhiên lớn hơn \(1\) và có nhiều hơn $2$ ước thì $a$ mới là hợp số nên B sai.
+) $1$ là số tự nhiên chỉ có $1$ ước là $1$ nên không là số nguyên tố và $0$ là số tự nhiên nhỏ hơn $1$ nên không là số nguyên tố. Lại có $0$ và $1$ đều không là hợp số do đó A đúng.
+) Số nguyên tố là số tự nhiên lớn hơn $1$ mà chỉ có hai ước là $1$ và chính nó nên D đúng và suy ra $2$ là số nguyên tố chẵn duy nhất nên C đúng.

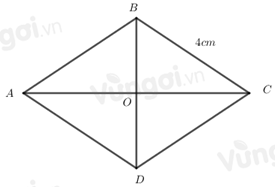
-
A.
\(AB = 2\,\,cm\)
-
B.
\(AD = 8\,\,cm\)
-
C.
\(DC = 4\,\,cm\)
-
D.
\(AB = 8\,\,cm\)
Đáp án : C
Hình thoi có bốn cạnh bằng nhau.
Hình thoi có bốn cạnh bằng nhau nên \(AB = BC = DC = AD = 4\,cm\).
=> \(DC = 4\,\,cm\).
Chọn câu đúng.
-
A.
\(\left( { - 20} \right).\left( { - 5} \right) = - 100\)
-
B.
\(\left( { - 50} \right).\left( { - 12} \right) = 600\)
-
C.
\(\left( { - 18} \right).25 = - 400\)
-
D.
\(11.\left( { - 11} \right) = - 1111\)
Đáp án : B
Áp dụng quy tắc nhân hai số nguyên cùng dấu, khác dấu để tính kết quả của từng đáp án và kết luận.
Đáp án A: \(\left( { - 20} \right).\left( { - 5} \right) = 100\) nên \(A\) sai.
Đáp án B: \(\left( { - 50} \right).\left( { - 12} \right) = 600\) nên \(B\) đúng.
Đáp án C: \(\left( { - 18} \right).25 = - 450 \ne - 400\) nên \(C\) sai.
Đáp án D: \(11.\left( { - 11} \right) = - 121 \ne - 1111\) nên \(D\) sai.
Cho n là một số tự nhiên lớn hơn 2 và nhỏ hơn 5. Khẳng định nào sau đây đúng ?
-
A.
n nằm bên phải điểm 5 trên tia số
-
B.
n nằm bên trái điểm 2 trên tia số
-
C.
n nằm bên phải điểm 2 trên tia số
-
D.
n nằm bên phải điểm 5 và cách điểm 5 một đơn vị trên tia số.
Đáp án : C
+ Vẽ tia số.
+ Số tự nhiên lớn hơn thì nằm bên phải, nhỏ hơn thì nằm bên trái.
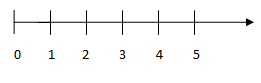
n là một số tự nhiên lớn hơn 2 nên n nằm bên phải điểm 2 => B sai, C đúng
n là một số tự nhiên nhỏ hơn 5 nên n nằm bên trái điểm 2 =>A,D sai.
Hình lục giác đều có mấy cạnh
-
A.
3
-
B.
5
-
C.
6
-
D.
8
Đáp án : C
Hình lục giác đều có 6 cạnh
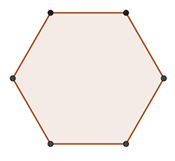
Cho diện tích tứ giác (1) bằng \(20\,\,c{m^2}\), Diện tích tam giác (2) bằng \(16\,\,c{m^2}\), Khi đó diện tích của hình trên bằng:

-
A.
\(36\,cm\)
-
B.
\(36\,d{m^2}\)
-
C.
\(26\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
Đáp án : D
Diện tích hình đã cho bằng tổng diện tích tứ giác (1) và (2).
Diện tích hình đã cho là: \(20 + 16 = 36\) (\(c{m^2}\)).
Cho bảng số liệu về các loại quả ưa thích của các bạn trong lớp 6A2 như sau
|
Các loại quả |
Cam |
Xoài |
Chuối |
Khế |
Ổi |
|
Số bạn thích |
8 |
9 |
6 |
4 |
3 |

Điền số mấy ở trên cột Khế?
-
A.
9
-
B.
8
-
C.
6
-
D.
4
Đáp án : D
Số trên cột Khế là số bạn thích khế.
Số bạn thích khế là 4 nên ta điền 4 trên cột Khế.
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Đáp án : A
Sử dụng dấu hiệu nhận biết hình chữ nhật
Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.
=> Đáp án B, C, D đúng.
Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ:
Điểm thi của Nam và Khải được biểu diễn trong biểu đồ cột kép ở hình sau:

Khẳng định nào sau đây đúng ?
-
A.
Điểm Toán của Nam cao hơn Khải
-
B.
Điểm cả 3 môn của Khải cao hơn Nam
-
C.
Điểm Ngữ văn của Nam cao hơn Khải
-
D.
Điểm Ngữ văn của Khải cao hơn Nam
Đáp án : C
- Lý thuyết về đọc biểu đồ tranh
- Cột màu vàng là điểm của Nam, màu xanh là điểm của Khải.
- Kiểm tra từng đáp án:
Điểm toán của Nam thấp hơn Khải => A sai.
Điểm Ngữ văn của Nam cao hơn Khải. Tức là điểm Ngữ văn của Khải thấp hơn Nam nên điểm 3 môn của Khải cao hơn Nam là sai
=> B sai, C đúng và D sai.
Hình thang cân có:
-
A.
1 cạnh bên
-
B.
2 cạnh bên
-
C.
3 cạnh bên
-
D.
4 cạnh bên
Đáp án : B
Sử dụng dấu hiệu nhận biết hình thang cân.
Hình thang cân có 2 cạnh bên.

Điền số thích hợp vào chỗ trống:
Kiểm tra thị lực của một học sinh trường THCS, ta thu được bảng kết quả như sau:
|
Khối |
Số học sinh được kiểm tra |
Số học sinh bị tật khúc xạ (cận thị, viễn thị, loạn thị) |
|
6 |
210 |
14 |
|
7 |
200 |
30 |
|
8 |
180 |
40 |
|
9 |
170 |
51 |
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
- Tính xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” từng khối.
Xác suất thực nghiệm=Số học sinh bị khúc xạ: Số học sinh được kiểm tra.
- So sánh các phân số với nhau.
Số học sinh bị khúc xạ khối 6 là 14. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là \(\dfrac{{14}}{{210}} = \dfrac{1}{{15}}\)
Số học sinh bị khúc xạ khối 7 là 30. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 7 là \(\dfrac{{30}}{{200}} = \dfrac{3}{{20}}\)
Số học sinh bị khúc xạ khối 8 là 40. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 8 là \(\dfrac{{40}}{{180}} = \dfrac{2}{9}\)
Số học sinh bị khúc xạ khối 9 là 51. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 9 là \(\dfrac{{51}}{{170}} = \dfrac{3}{{10}}\)
Số lớn nhất trong các số \(\dfrac{1}{{15}};\dfrac{3}{{20}};\dfrac{2}{9};\dfrac{3}{{10}}\) là \(\dfrac{3}{{10}}\).
Vậy khối có xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối 9
Tìm $x$ biết: $44 - x - 16{\rm{ }} = - 60$
-
A.
\(x = - 88\)
-
B.
\(x = - 42\)
-
C.
\(x = 42\)
-
D.
\(x = 88\)
Đáp án : D
Bước 1: Thu gọn vế trái Bước 2: Tìm x
Ta có $44 - x - 16{\rm{ }} = - 60$
\(\begin{array}{l}\left( {44 - 16} \right) - x = - 60\\28 - x = - 60\\x = 28 - \left( { - 60} \right)\\x = 28 + 60\\x = 88\end{array}\)
Vậy \(x = 88.\)
\(5125 + 456875\) bằng
-
A.
\(46200\)
-
B.
\(462000\)
-
C.
\(46300\)
-
D.
\(426000\)
Đáp án : B
Đặt tính rồi tính.

Vậy \(5125 + 456875 = 462000\)
5 là phần tử của
-
A.
Ư\(\left( {14} \right)\)
-
B.
Ư\(\left( {15} \right)\)
-
C.
Ư\(\left( {16} \right)\)
-
D.
Ư\(\left( {17} \right)\)
Đáp án : B
Ư \(\left( a \right)\) là tập hợp các ước của \(a\)
Nếu 5 là ước của \(a\) thì 5 là phần tử của Ư \(\left( a \right)\)
Ta có: Ư \(\left( {15} \right)\) là tập hợp các ước của 15.
Mà 5 là một ước của 15 nên 5 là phần tử của Ư \(\left( {15} \right)\)
Lan tìm hiểu về thức ăn sáng nay của các bạn trong lớp và thu được kết quả như sau:

Dữ liệu nào sau đây không là số liệu?
-
A.
Xôi
-
B.
11
-
C.
8
-
D.
2
Đáp án : A
Số liệu là các số.
Xôi không là số nên không là số liệu.
Tính \(3.\left( {{2^3}.4 - 6.5} \right)\)
-
A.
6
-
B.
3
-
C.
2
-
D.
1
Đáp án : A
Thực hiện phép tính trong ngoặc tròn ( ) trước: Lũy thừa \( \to \) nhân và chia \( \to \) cộng và trừ.
Lấy kết quả trong ngoặc nhân với 3.
\(3.\left( {{2^3}.4 - 6.5} \right) = 3.\left( {8.4 - 6.5} \right)\)\( = 3.\left( {32 - 30} \right) = 3.2 = 6\)
Một cửa hàng bán kính ghi lại số kính bán được trong tháng bằng bảng số liệu sau:
Số kính bán được trong tháng
|
Màu kính |
Trắng |
Đen |
Xanh |
Trắng bạc |
Vàng kim |
|
Số lượng |
20 |
10 |
30 |
15 |
25 |
Sử dụng các biểu tượng sau để vẽ biểu đồ tranh
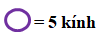
Cần bao nhiêu biểu tượng hình tròn màu tím để biểu diễn số kính màu vàng kim?
-
A.
25
-
B.
4
-
C.
5
-
D.
6
Đáp án : C
- Số hình tròn bằng số kính chia cho 5.
Màu trắng có 20 chiếc, ta vẽ 20:5=4 hình tròn.
Tương tự với màu đen, ta vẽ 2 hình, màu xanh ta vẽ 6 hình, màu trắng bạc ta vẽ 3 hình và màu vàng kim vẽ 5 hình.
Từ bảng thống kê, ta vẽ được biểu đồ tranh như sau:
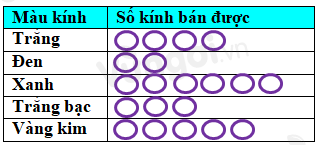
Hình chữ nhật có bao nhiêu trục đối xứng
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : B
Trục đối xứng của hình chữ nhật là đường thẳng đi qua trung điểm hai đáy.

Vậy hình chữ nhật có 2 trục đối xứng.
-
A.
Tổng của hai số nguyên cùng dấu là một số nguyên âm.
-
B.
Tổng của hai số nguyên âm là một số nguyên âm.
-
C.
Tổng của hai số nguyên cùng dấu là một số nguyên dương.
-
D.
Tổng của hai số nguyên dương là một số nguyên âm.
Đáp án : B
A và C sai do tổng của hai số nguyên cùng dấu có thể là số nguyên âm có thể là số nguyên dương
D sai vì tổng của hai số nguyên dương là một số nguyên dương
B đúng
Tập hợp các kết quả có thể xảy ra của phép thử nghiệm tung một đồng xu là
-
A.
\(X = \left\{ {N,S} \right\}\)
-
B.
\(X = \left\{ N \right\}\)
-
C.
\(X = \left\{ S \right\}\)
-
D.
\(X = \left\{ {NN,S} \right\}\)
Đáp án : A
Liệt kê các trường hợp của phép thử nghiệm tung đồng xu.
Phép thử nghiệm tung đồng xu có kết quả có thể là sấp (S) hoặc ngửa (N).
Vậy tập hợp các kết quả có thể xảy ra là \(X = \left\{ {N,S} \right\}\)
Viết tích \({a^4}.{a^6}\) dưới dạng một lũy thừa ta được
-
A.
\({a^8}\)
-
B.
\({a^9}\)
-
C.
\({a^{10}}\)
-
D.
\({a^2}\)
Đáp án : C
Sử dụng công thức nhân hai lũy thừa cùng cơ số ${a^m}.{a^n} = {a^{m + n}}$
Ta có \({a^4}.{a^6}\)\( = {a^{4 + 6}} = {a^{10}}\)
Tập hợp các số nguyên kí hiệu là
-
A.
$N$
-
B.
${N^*}$
-
C.
$Z$
-
D.
${Z^*}$
Đáp án : C
Tập hợp các số nguyên kí hiệu là $Z.$
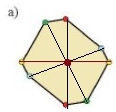
-
A.
Hình a
-
B.
Hình b
-
C.
Hình c
-
D.
Hình a và Hình c
Đáp án : A
Hình a có tâm đối xứng:
Kết quả của phép tính \(\left( {158.129 - 158.39} \right):180\) có chữ số tận cùng là
-
A.
\(8\)
-
B.
\(79\)
-
C.
\(9\)
-
D.
\(5\)
Đáp án : C
- Tính trong ngoặc bằng cách sử dụng \(ab - ac = a.\left( {b - c} \right).\)
- Thực hiện phép chia để tìm kết quả.
Ta có \(\left( {158.129 - 158.39} \right):180\)\( = 158.\left( {129 - 39} \right):180 = 158.90:180\)\( = 79.2.90:180 = 79.180:180 = 79.\)
Vậy kết quả của phép tính có chữ số tận cùng là \(9.\)
Gọi \({x_1}\) là giá trị thỏa mãn \({5^{x - 2}} - {3^2} = {2^4} - \left( {{2^8}{{.2}^4} - {2^{10}}{{.2}^2}} \right)\) và \({x_2}\) là giá trị thỏa mãn \(697:\left[ {\left( {15.x + 364} \right):x} \right] = 17\) . Tính \({x_1}.{x_2}\).
-
A.
$14$
-
B.
$56$
-
C.
$4$
-
D.
$46$
Đáp án : B
Tìm các giá trị \({x_1}\) và \({x_2}\) từ đó tính tích \({x_1}.{x_2}\)
\(\begin{array}{l}{\rm{ + )}}\,\,\,{5^{x - 2}} - {3^2} = {2^4} - \left( {{2^{8 + 4}} - {2^{10 + 2}}} \right)\\{5^{x - 2}} - {3^2} = {2^4} - \left( {{2^{12}} - {2^{12}}} \right)\\{5^{x - 2}} - {3^2} = {2^4} - 0 = {2^4}\\{5^{x - 2}} - 9 = 16\\{5^{x - 2}} = 16 + 9\\{5^{x - 2}} = 25\\{5^{x - 2}} = {5^2}\\x - 2\,\, = 2\\x\,\, = 2 + 2\\x = 4.\end{array}\)
\(\begin{array}{l}{\rm{ + )}}\,697:\left[ {\left( {15.x + 364} \right):x} \right] = 17\\\left( {15x + 364} \right):x = 697:17\\\left( {15x + 364} \right):x = 41\\15 + 364:x = 41\\364:x = 41 - 15\\364:x = 26\\x = 364:26\\x = 14\end{array}\)
Vậy \({x_1} = 4;\,{x_2} = 14\) nên \({x_1}.{x_2} = 4.14 = 56.\)
Tìm số tự nhiên \(\overline {145*} \) chia hết cho cả \(3\) và \(5.\)
-
A.
\(1454\)
-
B.
\(1450\)
-
C.
\(1455\)
-
D.
\(1452\)
Đáp án : C
+ Các số chia hết cho \(5\) có chữ số tận cùng là \(0\) hoặc \(5.\)
+ Các số chia hết cho \(3\) có tổng các chữ số chia hết cho \(3.\)
Từ đó lập luận để tìm các số thỏa mãn.
Vì \(\overline {145*} \) chia hết cho \(5\) nên \(*\) có thể bằng \(0\) hoặc \(5.\)
+ Nếu \(*\) bằng \(0\) thì ta được số \(1450\) có \(1 + 4 + 5 + 0 = 10\not \vdots 3\) nên loại
+ Nếu \(*\) bằng \(5\) thì ta được số \(1455\) có \(1 + 4 + 5 + 5 = 15 \vdots 3\) nên thỏa mãn.
Vậy số cần tìm là \(1455.\)
Một căn phòng hình chữ nhật dài $680$cm, rộng $480$cm. Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Hỏi viên gạch có độ dài lớn nhất là bao nhiêu?
-
A.
$5\,cm$
-
B.
$10\,cm$
-
C.
$20\,cm$
-
D.
$40\,cm$
Đáp án : D
Vì muốn lát gạch kín căn phòng mà không có viên gạch nào bị cắt xén thì độ dài cạnh viên gạch phải là ước của $680$ và $480.$ Để viên gạch có độ dài lớn nhất thì đồ dài cạnh viên gạch bằng ƯCLN$\left( {680;480} \right).$
Ta có: Gọi chiều dài viên gạch là $x.$ Để lát kín căn phòng mà không có có viên gạch nào bị cắt xén thì $x$ phải là ước của chiều dài và chiều rộng căn phòng Hay $680 \, \vdots \, x$ và $480 \, \vdots \, x$ $ \Rightarrow x \in $ ƯC$\left( {680;480} \right)$ Để x là lớn nhất $ \Rightarrow x = $ƯCLN$\left( {680;480} \right)$ Ta có: $680 = {2^3}.5.17;$ $480 = {2^5}.3.5$ $ \Rightarrow x = $ ƯCLN$\left( {680;480} \right)$$ = {2^3}.5 = 40$ Vậy để lát kín căn phòng mà không có viên gạch nào bị cắt xén thì độ dài cạnh viên gạch lớn nhất là $40$ $cm.$
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ \(800\) đến \(900\) em.
-
A.
$845$
-
B.
$840$
-
C.
$860$
-
D.
$900$
Đáp án : A
+ Sử dụng kiến thức về phép chia có dư.
+ Sử dụng kiến thức về bội chung và bội chung nhỏ nhất.
+ Sử dụng cách tìm bội chung thông qua bội chung nhỏ nhất.
Gọi số học sinh đi thăm quan là \(x\,\left( {x \in {N^*};\,800 \le x \le 900} \right)\) (học sinh)
Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi nghĩa là thừa ra 5 học sinh nên ta có
\(\left( {x - 5} \right) \vdots 35;\,\left( {x - 5} \right) \vdots 40\) suy ra \(\left( {x - 5} \right) \in BC\left( {35;40} \right)\).
Ta có \(35 = 5.7;\,40 = {2^3}.5\) nên \(BCNN\left( {35;40} \right) = {2^3}.5.7 = 280.\)
Suy ra \((x-5) \in BC\left( {35;40} \right) = B\left( {280} \right) = \left\{ {280;560;840;1120;...} \right\}\) mà \(800 \le x \le 900\) nên \(x -5= 840\) hay $x=845.$
Vậy số học sinh đi thăm quan là \(845\) học sinh.
Biết \( - 9 < x < 0\). Tập hợp các số nguyên $x$ thỏa mãn:
-
A.
\(A = \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\)
-
B.
\(A = \left\{ { - 9; - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\)
-
C.
\(A = \left\{ { - 9; - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1;0} \right\}\)
-
D.
\(A = \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1;0} \right\}\)
Đáp án : A
Vì $x$ là số nguyên nên dựa vào điều kiện đề bài ta tìm được giá trị của $x$ và viết chúng dưới dạng tập hợp.
Vì \( - 9 < x < 0;x \in Z \Rightarrow x \in \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\)
Do đó \(A = \left\{ { - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1} \right\}\).
-
A.
\( - 2021;\,\, - 10;\,\,4;\,0;\, - 1\)
-
B.
\( - 2021;\,\, - 10;\,\, - 1;\,\,0;\,\,4\)
-
C.
\( - 2021;\,\, - 10;\,\,0;\,\, - 1;\,\,4\)
-
D.
\(4;\,0;\, - 1;\, - 10;\, - 2021\)
Đáp án : B
- So sánh các số
- Sắp xếp các số nguyên theo thứ tự tăng dần tức là số nào nhỏ hơn ta viết trước, số lớn hơn ta viết sau.
Ta có: \( - 2021 < \, - 10 < \, - 1 < \,\,0 < \,\,4\).
Sắp xếp theo thứ tự tăng dần: \( - 2021;\,\, - 10;\,\, - 1;\,\,0;\,\,4\)

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:
A. \(16cm\)
B. \(17cm\)
C. \(18cm\)
D. \(19cm\)
C. \(18cm\)
Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính độ dài cạnh đáy \(a\) là \(a = S:h\).
Độ dài đáy của hình bình hành đó là:
\(432:24 = 18\,\,(cm)\)
Đáp số: \(18cm\).
-
A.
Tam giác đều
-
B.
Cánh quạt
-
C.
Trái tim
-
D.
Cánh diều
Đáp án : B
Hình có tâm đối xứng là hình cánh quạt (Tâm đối xứng là tâm của đường tròn nhỏ phía trong)
Tìm các giá trị thích hợp của chữ số $a$ sao cho: \( - \overline {a99} > - 649 > - \overline {6a0} \)
-
A.
$6$
-
B.
$5$
-
C.
$4$
-
D.
$7$
Đáp án : B
Dựa vào việc so sánh hai số nguyên:
+ Với \(a,b \in Z\), nếu điểm $a$ nằm bên trái điểm $b$ trên trục số nằm ngang thì \(a < b\)
+ Số nguyên $b$ là số liền sau của số nguyên $a$ nếu \(a < b\) và giữa $a$ và $b$ không có số nguyên nào nữa.
\( - \overline {a99} > - 649 > - \overline {6a0} \Rightarrow \overline {a99} < 649 < \overline {6a0} \Rightarrow \left\{ \begin{array}{l}a < 6\\4 < a\end{array} \right. \Rightarrow 4 < a < 6\).
Mà \(a \in {N^*}\) nên \(a = 5\).
Toán vui. Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí nhìn khác nhau nên hai bạn thấy hai dãy các phép tính khác nhau.

Phép tính Toàn quan sát được để phép tính hai bạn quan sát thấy bằng nhau là:
-
A.
\({\bf{11}} + {\bf{8}}1 + 1{\bf{9}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{270}} \)
-
B.
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{275}} \)
-
C.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
-
D.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{6}}8 + {\bf{9}}1 + 11{\rm{ }} = {\bf{344}} \)
Đáp án : C
Điền các số: 1; 6; 8; 9 vào ô trống để được phép tính đúng.
Phép tính Toàn quan sát được là:
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
Phép tính Na quan sát được là:
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{69}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{344}} \)
Cho phép tính \(\overline {ab} .\,c\, = 424.\) Khi đó \(c\) bằng bao nhiêu?
-
A.
$9$
-
B.
$8$
-
C.
$5$
-
D.
$6$
Đáp án : B
Phân tích số \(424\) ra thừa số nguyên tố, sau đó tìm các ước có hai chữ số và một chữ số của \(424\).
Từ đó tìm được \(\overline {ab} \) và \(c.\)
Vì \(\overline {ab} .\,c\, = 424\) nên \(\overline {ab} \) là ước có hai chữ số của \(424.\)
Phân tích số \(424\) ra thừa số nguyên tố ta được

Hay \(424 = {2^3}.53\)
Các ước của \(424\) là \(1;2;4;8;53;106;212;424\)
Suy ra \(\overline {ab} = 53\) suy ra \(c = 424:53 = 8.\)
Chọn câu đúng nhất.
-
A.
\(\left( {a - b} \right) + \left( {c - d} \right) - \left( {a + c} \right) = - \left( {b + d} \right)\)
-
B.
\(\left( {a - b} \right) - \left( {c - d} \right) + \left( {b + c} \right) = a + d\)
-
C.
\(\left( {a - b} \right) - \left( {c - d} \right) + \left( {b - a} \right) = - \left( {c - d} \right)\)
-
D.
Cả A, B, C đều đúng
Đáp án : D
Bỏ dấu ngoặc, rút gọn từng biểu thức và kết luận đáp án đúng.
\(\begin{array}{l}\left( {a - b} \right) + \left( {c - d} \right) - \left( {a + c} \right)\\ = a - b + c - d - a - c\\ = \left( {a - a} \right) - b + \left( {c - c} \right) - d\\ = - b - d\\ = - \left( {b + d} \right)\end{array}\)
Do đó \(A\) đúng.
Đáp án B:
\(\begin{array}{l}\left( {a - b} \right) - \left( {c - d} \right) + \left( {b + c} \right)\\ = a - b - c + d + b + c\\ = a - \left( {b - d} \right) - \left( {c - c} \right) + d\\ = a + d\end{array}\)
Nên \(B\) đúng.
Đáp án C:
\(\begin{array}{l}\left( {a - b} \right) - \left( {c - d} \right) + \left( {b - a} \right)\\ = a - b - c + d + b - a\\ = \left( {a - a} \right) - \left( {b - b} \right) - c + d\\ = - c + d\\ = - \left( {c - d} \right)\end{array}\)
Nên \(C\) đúng.
Vậy cả ba đáp án A, B, C đều đúng.
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
-
A.
\(6\)
-
B.
\(46\)
-
C.
\(16\)
-
D.
\(5\)
Đáp án : C
+ Biến đổi để tách \(5x + 46y\) thành tổng của hai số, trong đó một số chia hết cho $16$ và một số chứa nhân tử \(x + 6y\)
+ Sử dụng tính chất chia hết trên tập hợp các số nguyên để chứng minh.
Ta có:
\(\begin{array}{l}5x + 46y = 5x + 30y + 16y\\ = \left( {5x + 30y} \right) + 16y\\ = 5\left( {x + 6y} \right) + 16y\end{array}\)
Vì \(5x + 46y\) chia hết cho $16$ và $16y$ chia hết cho $16$ nên suy ra \(5\left( {x + 6y} \right)\) chia hết cho $16.$
Mà $5$ không chia hết cho $16$ nên suy ra \(x + 6y\) chia hết cho $16$
Vậy nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) cũng chia hết cho $16.$