Đề kiểm tra học kì 1 Toán 6 Cánh diều - Đề số 3
Đề bài
Chọn câu sai.
-
A.
$\left( { - 2} \right) + \left( { - 5} \right) > 0$
-
B.
$\left( { - 3} \right) + \left( { - 4} \right) = \left( { - 2} \right) + \left( { - 5} \right)$
-
C.
$\left( { - 6} \right) + \left( { - 1} \right) < - 6$
-
D.
$\left| {\left( { - 1} \right) + \left( { - 2} \right)} \right| = 3$
-
A.
\( - 46718 < - 46812\)
-
B.
\( - 67523 < - 66712\)
-
C.
\( - 12 > 7\)
-
D.
\( - 123 < - 126\)
Trong các phát biểu sau đây, phát biểu nào đúng ?
-
A.
\( - 24\) chia hết cho \(5\)
-
B.
\(36\) không chia hết cho \( - 12\)
-
C.
\( - 18\) chia hết cho \( - 6\)
-
D.
\( - 26\) không chia hết cho \( - 13\)
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
Thu gọn biểu thức \(z - (x + y - z) - \left( { - x} \right)\) ta được:
-
A.
\(2y - x\)
-
B.
\(y - 2x\)
-
C.
\(2z - y\)
-
D.
\(y\)
Phân tích số \(a\) ra thừa số nguyên tố \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\), khẳng định nào sau đây là đúng:
-
A.
Các số \({p_1};\,{p_2};...;\,{p_k}\) là các số dương.
-
B.
Các số \({p_1};\,{p_2};...;\,{p_k} \in P\)(với $P$ là tập hợp các số nguyên tố).
-
C.
Các số \({p_1};\,{p_2};...;\,{p_k} \in N\).
-
D.
Các số \({p_1};\,{p_2};...;\,{p_k}\) tùy ý.
Hình thang cân có:
-
A.
1 cạnh bên
-
B.
2 cạnh bên
-
C.
3 cạnh bên
-
D.
4 cạnh bên
-
A.
Cầu lông, bóng bàn, đá cầu, bóng rổ, bóng đá
-
B.
Bóng chuyền, bóng bàn, bóng đá, đá cầu, bóng rổ
-
C.
Đá cầu, bóng chuyền, điền kinh, bóng rổ, bóng bàn
-
D.
Bóng rổ, đá cầu, bóng đá
-
A.
FC=3cm
-
B.
AD= 3cm
-
C.
BE= 3cm
-
D.
EF=3cm
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Cho \(246 + 388 = 634\).
Vậy \(388 + 246 =\)
Sau khi phân tích 45, 150 ra các thừa số nguyên tố được 45 = 3 2 .5 và 150 = 2.3.5 2 . Số mũ nhỏ nhất của thừa số chung 3 là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
Cho \(\overline {17*} \) chia hết cho 2. Số thay thế cho * có thể là
-
A.
1
-
B.
2
-
C.
3
-
D.
5
Viết tập hợp sau bằng cách liệt kê các phần tử: \(A = \left\{ {a \in \mathbb{N}^*\left| {a < 5} \right.} \right\}\)
-
A.
\(A = \left\{ {0;1;2;3;4} \right\}\)
-
B.
\(A = \left\{ {0,1,2,3,4,5} \right\}\)
-
C.
\(A = \left\{ {1;2;3;4;5} \right\}\)
-
D.
\(A = \left\{ {1;2;3;4} \right\}\)
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
-
A.
$a = 5$
-
B.
$a = 13$
-
C.
$a = - 13$
-
D.
$a = 9$
-
A.
Hình a, b, c
-
B.
Hình a, c, d
-
C.
Hình a,d
-
D.
Cả bốn hình
Số $x$ là bội chung của ${\rm{a;b;c}}$ nếu:
-
A.
$x \, \vdots \, a$ hoặc $x \, \vdots \, b$ hoặc $x \, \vdots \, c$
-
B.
$x \, \vdots \, a$ và $x \, \vdots \, b$
-
C.
$x \, \vdots \, b$ và $x \, \vdots \, c$
-
D.
$x \, \vdots \, a$ và $x \, \vdots \, b$ và $x \, \vdots \, c$
Trong một hộp có 1 quả bóng xanh và 9 bóng vàng có kích thước giống nhau. An lấy ra đồng thời 2 bóng từ hộp. Có các sự kiện sau:
1- An lấy được 2 bóng màu xanh
2- An lấy được ít nhất một bóng màu vàng
3- An lấy được 2 bóng màu vàng.
Sự kiện chắc chắn, không thể và có thể xảy ra lần lượt là
-
A.
1-2-3
-
B.
2-3-1
-
C.
3-2-1
-
D.
2-1-3
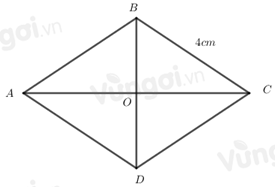
-
A.
\(AB = 2\,\,cm\)
-
B.
\(AD = 8\,\,cm\)
-
C.
\(DC = 4\,\,cm\)
-
D.
\(AB = 8\,\,cm\)
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
-
A.
87 triệu dân
-
B.
8 triệu dân
-
C.
79 triệu dân
-
D.
10 triệu dân
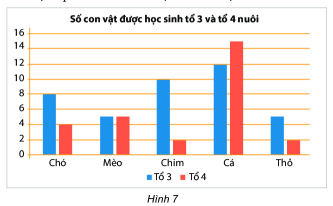
-
A.
Tổ 3 là 10, tổ 4 là 14
-
B.
Tổ 3 là 12, tổ 4 là 16
-
C.
Tổ 3 là 12, tổ 4 là 15
-
D.
Tổ 3 là 15, tổ 4 là 12
+) Tích ba số nguyên âm là một số nguyên ..(1)..
+) Tích hai số nguyên âm với một số nguyên dương là một số nguyên …(2)…
Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:
-
A.
âm, âm
-
B.
dương, âm
-
C.
âm, dương
-
D.
dương, dương
Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần |
8 |
7 |
3 |
12 |
10 |
10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
-
A.
0,21
-
B.
0,44
-
C.
0,42
-
D.
0,18
Khẳng định nào sau đây đúng ?
-
A.
B\(\left( 2 \right) = \left\{ {0,2,4,6,8,...} \right\}\)
-
B.
B\(\left( 2 \right) = \left\{ {0;2;4;6;8;...} \right\}\)
-
C.
B \(\left( 2 \right) = \left\{ {2;4;6;8;...} \right\}\)
-
D.
B\(\left( 2 \right) = \left\{ {1;2;4;6;8;...} \right\}\)
-
A.
Số đối của một số nguyên dương là một số nguyên âm.
-
B.
Số \(0\) không có số đối.
-
C.
Số đối của mọi số nguyên dương đều là số nguyên dương.
-
D.
Số đối của mọi số nguyên âm đều là số nguyên âm.
Kết quả của phép trừ: \(\left( { - 47} \right) - 53\) là:
-
A.
\(6\)
-
B.
\( - 6\)
-
C.
\(100\)
-
D.
\( - 100\)
Viết tập hợp \(A = \left\{ {16;17;18;19} \right\}\) dưới dạng chỉ ra tính chất đặc trưng.
-
A.
\(A = \left\{ {x \in N|15 < x < 19} \right\}\)
-
B.
\(A = \left\{ {x\in N |15 < x < 20} \right\}\)
-
C.
\(A = \left\{ {x\in N |16 < x < 20} \right\}\)
-
D.
\(A = \left\{ {x\in N |15 < x \le 20} \right\}\)
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là
-
A.
\(2k + 5\,\left( {k \in N} \right)\)
-
B.
\(5k + 2\,\left( {k \in N} \right)\)
-
C.
\(2k\,\left( {k \in N} \right)\)
-
D.
\(5k + 4\,\left( {k \in N} \right)\)
-
A.
Hình a) và c) có trục đối xứng
-
B.
Hình c) có trục đối xứng
-
C.
Hình b) và c) có trục đối xứng
-
D.
Cả 3 hình có trục đối xứng
 Chọn dấu thích hợp để điền vào chỗ chấm:
Chọn dấu thích hợp để điền vào chỗ chấm:
$1675 + 2468 + 325\;...\;321 + 2178 + 1822$
A. \( = \)
B. \( < \)
C. \( > \)
Gọi \(x\) là số tự nhiên thỏa mãn \({2^x} - 15 = 17\). Chọn câu đúng.
-
A.
\(x < 6\)
-
B.
\(x > 7\)
-
C.
\(x < 5\)
-
D.
\(x < 4\)
Cho \(A = 4.\left\{ {{3^2}.\left[ {\left( {{5^2} + {2^3}} \right):11} \right] - 26} \right\} + 2002\) và \(B = 134 - \left\{ {150:5 - \left[ {120:4 + 25 - \left( {12 + 18} \right)} \right]} \right\}\). Chọn câu đúng.
-
A.
$A = B$
-
B.
$A = B + 1$
-
C.
$A < B$
-
D.
$A > B$
Mỗi người khi ăn thì sẽ hấp thụ ca-lo và khi hoạt động thì sẽ tiêu hao ca-lo. Bạn Bình dùng phép cộng số nguyên để tính số ca-lo hằng ngày của mình bằng cách xem số ca-lo hấp thụ là số nguyên dương và số ca-lo tiêu hao là số nguyên âm. Em hãy giúp bạn Bình kiểm tra tổng số ca-lo còn lại sau khi ăn sáng và thực hiện các hoạt động (theo số liệu trong bảng dưới đây).

-
A.
\( - 189\)
-
B.
\( 389\)
-
C.
\( - 389\)
-
D.
\( 289\)
Hình nào sau đây không có tâm đối xứng
-
A.
Hình vuông
-
B.
Hình chữ nhật
-
C.
Hình bình hành
-
D.
Hình tam giác đều
Biểu đồ tranh dưới đây cho biết số học sinh nữ của các lớp khối 6 trường THCS Hoàng Việt.
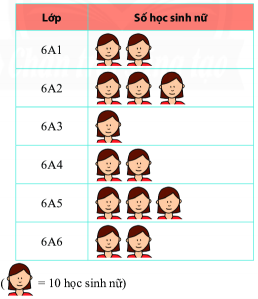
Em hãy quan sát biểu đồ tranh ở trên và chọn đáp án đúng
-
A.
Lớp 6A1 có ít học sinh nữ nhất
-
B.
Lớp 6A4 có nhiều học sinh nữ hơn lớp 6A5
-
C.
Lớp 6A6 có 20 học sinh nữ.
-
D.
Tổng số học sinh nữ của các lớp khối 6 là 120 học sinh
Tìm giá trị lớn nhất của biểu thức: \(C = - {\left( {x - 5} \right)^2} + 10\)
-
A.
\( - 10\)
-
B.
\(5\)
-
C.
\(0\)
-
D.
\(10\)
Toán vui. Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí nhìn khác nhau nên hai bạn thấy hai dãy các phép tính khác nhau.

Phép tính Toàn quan sát được để phép tính hai bạn quan sát thấy bằng nhau là:
-
A.
\({\bf{11}} + {\bf{8}}1 + 1{\bf{9}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{270}} \)
-
B.
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{275}} \)
-
C.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
-
D.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{6}}8 + {\bf{9}}1 + 11{\rm{ }} = {\bf{344}} \)
Số \(A = \overline {abcd} - \left( {a + b + c + d} \right)\) chia hết cho số nào dưới đây?
-
A.
\(2\)
-
B.
\(5\)
-
C.
\(9\)
-
D.
\(6\)
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
-
A.
5000 cm
-
B.
10000 cm
-
C.
2500 cm 2
-
D.
5000 cm 2
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
-
A.
Hai số trên có hai ước chung
-
B.
Hai số trên có ba ước chung
-
C.
Hai số trên là hai số nguyên tố cùng nhau
-
D.
Hai số trên chỉ có một ước chung là 3.
Lời giải và đáp án
Chọn câu sai.
-
A.
$\left( { - 2} \right) + \left( { - 5} \right) > 0$
-
B.
$\left( { - 3} \right) + \left( { - 4} \right) = \left( { - 2} \right) + \left( { - 5} \right)$
-
C.
$\left( { - 6} \right) + \left( { - 1} \right) < - 6$
-
D.
$\left| {\left( { - 1} \right) + \left( { - 2} \right)} \right| = 3$
Đáp án : A
Sử dụng cách cộng hai số nguyên cùng dấu để tính toán và so sánh các kết quả thu được
Chú ý đến cách tính giá trị tuyệt đối của một số: \(\left| a \right|=\left\{ \begin{array}{l}a\,\,\,\,\,\,{\rm{khi}}\,a \ge 0\\ - a\,\,{\rm{khi}}\,a < 0\end{array} \right.\) .
+) Ta có $\left( { - 2} \right) + \left( { - 5} \right) = - \left( {2 + 5} \right) = - 7 < 0$ nên A sai.
+) Ta có \(\left( { - 3} \right) + \left( { - 4} \right) = - \left( {3 + 4} \right) = - 7\) và \(\left( { - 2} \right) + \left( { - 5} \right) = - 7\) nên \(\left( { - 3} \right) + \left( { - 4} \right) = \left( { - 2} \right) + \left( { - 5} \right)\). Do đó B đúng.
+) Ta có \(\left( { - 6} \right) + \left( { - 1} \right) = - \left( {6 + 1} \right) = - 7 < - 6\) nên C đúng.
+) Ta có \(\left| {\left( { - 1} \right) + \left( { - 2} \right)} \right| = \left| { - \left( {1 + 2} \right)} \right| = \left| { - 3} \right| = 3\) nên D đúng.
-
A.
\( - 46718 < - 46812\)
-
B.
\( - 67523 < - 66712\)
-
C.
\( - 12 > 7\)
-
D.
\( - 123 < - 126\)
Đáp án : B
- Số nguyên âm luôn nhỏ hơn số nguyên dương.
- Để so sánh hai số nguyên âm, ta làm như sau:
Bước 1: Bỏ dấu “-” trước cả hai số âm.
Bước 2: Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (tương ứng) sẽ lớn hơn.
Do \(67523 > 66712\) nên \( - 67523 < - 66712\).
Khẳng định đúng là: B
Trong các phát biểu sau đây, phát biểu nào đúng ?
-
A.
\( - 24\) chia hết cho \(5\)
-
B.
\(36\) không chia hết cho \( - 12\)
-
C.
\( - 18\) chia hết cho \( - 6\)
-
D.
\( - 26\) không chia hết cho \( - 13\)
Đáp án : C
Cho \(a,b \in \mathbb{Z}\) và \(b \ne 0\) . Nếu có số nguyên \(q\) sao cho \(a = bq\) thì:
Ta nói \(a\) chia hết cho \(b\) , kí hiệu là \(a \vdots b\) .
Ta có: \( - 18 = \left( { - 6} \right).3\) nên \( - 18\) chia hết cho \( - 6\) => C đúng
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
Đáp án : A
- Áp dụng kiến thức:
Mọi số tự nhiên đều có ước là $1$.
Số nguyên tố có $2$ ước là $1$ và chính nó.
Mọi số nguyên tố khác nhau đều có ước chung duy nhất là $1$.
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$.
B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.
C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.
D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.
Thu gọn biểu thức \(z - (x + y - z) - \left( { - x} \right)\) ta được:
-
A.
\(2y - x\)
-
B.
\(y - 2x\)
-
C.
\(2z - y\)
-
D.
\(y\)
Đáp án : C
Khi bỏ dấu ngoặc, nếu đằng trước dấu ngoặc:
Có dấu “-”, thì phải đổi dấu tất cả các số hạng trong ngoặc
\( - \left( {a + b - c} \right) = - a - b + c\)
\(\begin{array}{l}z - (x + y - z) - \left( { - x} \right) = z - x - y + z + x\\ = \left( { - x + x} \right) + \left( {z + z} \right) - y\\ = 0 + 2z - y\\ = 2z - y\end{array}\)
Phân tích số \(a\) ra thừa số nguyên tố \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\), khẳng định nào sau đây là đúng:
-
A.
Các số \({p_1};\,{p_2};...;\,{p_k}\) là các số dương.
-
B.
Các số \({p_1};\,{p_2};...;\,{p_k} \in P\)(với $P$ là tập hợp các số nguyên tố).
-
C.
Các số \({p_1};\,{p_2};...;\,{p_k} \in N\).
-
D.
Các số \({p_1};\,{p_2};...;\,{p_k}\) tùy ý.
Đáp án : B
- Áp dụng kiến thức về phân tích $1$ số thành thừa số nguyên tố (các thừa số trong tích phải là số nguyên tố)
Khi phân tích một số \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\) ra thừa số nguyên tố thì các số \({p_1},{p_2},...,{p_k}\) phải là các số nguyên tố.
Hình thang cân có:
-
A.
1 cạnh bên
-
B.
2 cạnh bên
-
C.
3 cạnh bên
-
D.
4 cạnh bên
Đáp án : B
Sử dụng dấu hiệu nhận biết hình thang cân.
Hình thang cân có 2 cạnh bên.
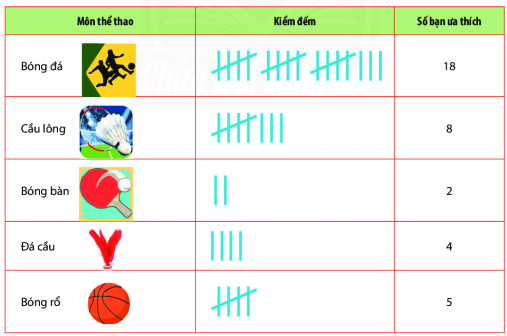
-
A.
Cầu lông, bóng bàn, đá cầu, bóng rổ, bóng đá
-
B.
Bóng chuyền, bóng bàn, bóng đá, đá cầu, bóng rổ
-
C.
Đá cầu, bóng chuyền, điền kinh, bóng rổ, bóng bàn
-
D.
Bóng rổ, đá cầu, bóng đá
Đáp án : A
Nhận xét về tên các môn thể thao được yêu thích của lớp 6A và số lượng các bạn ưa thích các môn thể thao đó.
Các môn thể thao được yêu thích của lớp 6A là: Bóng đá, cầu lông, bóng bàn, đá cầu, bóng rổ.
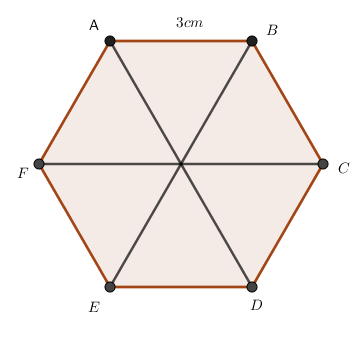
-
A.
FC=3cm
-
B.
AD= 3cm
-
C.
BE= 3cm
-
D.
EF=3cm
Đáp án : D
Lục giác đều có các cạnh bằng nhau nên AB=EF=3cm
Các đoạn thẳng AD, BE, FC là các đường chéo chính nên không bằng cạnh bên.
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Cho \(246 + 388 = 634\).
Vậy \(388 + 246 =\)
Cho \(246 + 388 = 634\).
Vậy \(388 + 246 =\)
Áp dụng tính chất giao hoán của phép cộng: Khi đổi chỗ các số hạng trong một tổng thì tổng đó không thay đổi: \(a + b = b + a\)
Ta có: \(246 + 388 = 388 + 246\)
Mà \(246 + 388 = 634\) nên \(388 + 246 = 634\).
Vậy đáp án đúng điền vào ô trống là \(634\).
Sau khi phân tích 45, 150 ra các thừa số nguyên tố được 45 = 3 2 .5 và 150 = 2.3.5 2 . Số mũ nhỏ nhất của thừa số chung 3 là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
Đáp án : A
Xác định số mũ của thừa số 3 trong hai số 45 và 150.
Chọn ra số nhỏ nhất làm số mũ nhỏ nhất.
45 = 3 2 .5 nên số mũ của 3 là 2
150 = 2.3.5 2 nên số mũ của 3 là 1
Số nhỏ nhất là 1 nên số mũ nhỏ nhất của thừa số chung 3 khi phân tích 45 và 150 ra tích các thừa số nguyên tố là 1.
Cho \(\overline {17*} \) chia hết cho 2. Số thay thế cho * có thể là
-
A.
1
-
B.
2
-
C.
3
-
D.
5
Đáp án : B
Vị trí của * là chữ số tận cùng.
Các số có chữ số tận cùng là số chẵn \(\left( {0,{\rm{ }}2,{\rm{ }}4,{\rm{ }}6,{\rm{ }}8} \right)\) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
Vì * là chữ số tận cùng của \(\overline {17*} \) nên * chỉ có thể là 0;2;4;6;8.
Vậy số 2 là số cần tìm.
Viết tập hợp sau bằng cách liệt kê các phần tử: \(A = \left\{ {a \in \mathbb{N}^*\left| {a < 5} \right.} \right\}\)
-
A.
\(A = \left\{ {0;1;2;3;4} \right\}\)
-
B.
\(A = \left\{ {0,1,2,3,4,5} \right\}\)
-
C.
\(A = \left\{ {1;2;3;4;5} \right\}\)
-
D.
\(A = \left\{ {1;2;3;4} \right\}\)
Đáp án : D
Tìm các số tự nhiên nhỏ hơn 5 và khác 0.
\(\mathbb{N}^*\) là tập hợp các số tự nhiên khác 0.
Các số tự nhiên nhỏ hơn 5 là 0;1;2;3;4
Vì \(a \in \mathbb{N}^*\) nên a khác 0, do đó các phần tử của $A$ là $1;2;3;4$.
Vậy \(A = \left\{ {1;2;3;4} \right\}\)
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
-
A.
$a = 5$
-
B.
$a = 13$
-
C.
$a = - 13$
-
D.
$a = 9$
Đáp án : A
+ Bước 1: Tìm ước của \(9\) + Bước 2: Tìm $a$ và kết luận giá trị lớn nhất của \(a\)
$a + 4$ là ước của $9$ $ \Rightarrow \;\left( {a + 4} \right) \in U\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\;$ Ta có bảng giá trị như sau:

Vậy giá trị lớn nhất của \(a\) là \(a = 5\)
-
A.
Hình a, b, c
-
B.
Hình a, c, d
-
C.
Hình a,d
-
D.
Cả bốn hình
Đáp án : B
Mỗi hình có một điểm O, mà khi quay hình đó xung quanh điểm O đúng một nửa vòng thì hình thu được chồng khít" với chính nó ở vị trí ban đầu (trước khi quay).
- Hình b) là hình không có tâm đối xứng.
- Hình a), hình c) và hình d) là các hình có tâm đối xứng.
Số $x$ là bội chung của ${\rm{a;b;c}}$ nếu:
-
A.
$x \, \vdots \, a$ hoặc $x \, \vdots \, b$ hoặc $x \, \vdots \, c$
-
B.
$x \, \vdots \, a$ và $x \, \vdots \, b$
-
C.
$x \, \vdots \, b$ và $x \, \vdots \, c$
-
D.
$x \, \vdots \, a$ và $x \, \vdots \, b$ và $x \, \vdots \, c$
Đáp án : D
- Sử dụng kiến thức bội chung $2$ hay nhiều số: bội chung của $2$ hay nhiều số là bội của tất cả các số đó.
Số \(x\) là bội chung của $3$ số $a,b,c$ nếu \(x\) chia hết cho cả \(a,b,c\).
Trong một hộp có 1 quả bóng xanh và 9 bóng vàng có kích thước giống nhau. An lấy ra đồng thời 2 bóng từ hộp. Có các sự kiện sau:
1- An lấy được 2 bóng màu xanh
2- An lấy được ít nhất một bóng màu vàng
3- An lấy được 2 bóng màu vàng.
Sự kiện chắc chắn, không thể và có thể xảy ra lần lượt là
-
A.
1-2-3
-
B.
2-3-1
-
C.
3-2-1
-
D.
2-1-3
Đáp án : D
Tìm tất cả các kết quả có thể xảy ra trong mỗi lần lấy bóng.
Sự kiện chắc chắn xảy ra: Luôn xảy ra.
Sự kiện không thể xảy ra: Không bao giờ xảy ra
Sự kiện có thể xảy ra: Lúc xảy ra, lúc không xảy ra.
Các kết quả có thể xảy ra là: (1 xanh + 1 vàng) ; (2 vàng).
Cả hai kết quả này luôn có xuất hiện quả màu vàng nên sự kiện 2 chắc chắn xảy ra.
Ta không bao giờ có thể lấy được 2 quả bóng màu xanh cùng một lúc được vì tổng số bóng xanh chỉ có 1 quả. Sự kiện 1 là sự kiện không thể xảy ra.
Trong hai kết quả trên có một kết quả là 2 vàng nên sự kiện 3 có thể xảy ra.
Vậy sự kiện chắc chắn, không thể và có thể xảy ra lần lượt là 2-1-3.

-
A.
\(AB = 2\,\,cm\)
-
B.
\(AD = 8\,\,cm\)
-
C.
\(DC = 4\,\,cm\)
-
D.
\(AB = 8\,\,cm\)
Đáp án : C
Hình thoi có bốn cạnh bằng nhau.
Hình thoi có bốn cạnh bằng nhau nên \(AB = BC = DC = AD = 4\,cm\).
=> \(DC = 4\,\,cm\).
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Đáp án : A
Sử dụng dấu hiệu nhận biết hình chữ nhật
Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.
=> Đáp án B, C, D đúng.
Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ:
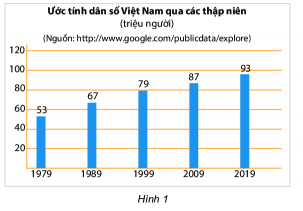
-
A.
87 triệu dân
-
B.
8 triệu dân
-
C.
79 triệu dân
-
D.
10 triệu dân
Đáp án : B
Quan sát biểu đồ cột và xác định số dân năm 1999 và 2009.
Số dân tăng: Lấy số dân năm 2009 trừ đi số dân năm 1999.
Dân số Việt Nam năm 1999 là 79 triệu người và năm 2009 là 87 triệu người.
Dân số từ 1999 đến 2009 tăng 87-79=8 triệu người.
-
A.
Tổ 3 là 10, tổ 4 là 14
-
B.
Tổ 3 là 12, tổ 4 là 16
-
C.
Tổ 3 là 12, tổ 4 là 15
-
D.
Tổ 3 là 15, tổ 4 là 12
Đáp án : C
- Tổ 3: Màu xanh
- Tổ 4: Màu đỏ
Số cá tổ 3: 12
Số cá tổ 4: 15
+) Tích ba số nguyên âm là một số nguyên ..(1)..
+) Tích hai số nguyên âm với một số nguyên dương là một số nguyên …(2)…
Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:
-
A.
âm, âm
-
B.
dương, âm
-
C.
âm, dương
-
D.
dương, dương
Đáp án : C
- Tích của hai số nguyên trái dấu là số nguyên âm.
- Tính của hai số nguyên cùng dấu là số nguyên dương.
Tích ba số nguyên âm là một số nguyên âm.
Tích hai số nguyên âm với một số nguyên dương là một số nguyên dương
Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần |
8 |
7 |
3 |
12 |
10 |
10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
-
A.
0,21
-
B.
0,44
-
C.
0,42
-
D.
0,18
Đáp án : C
- Xác định các mặt có số lẻ chấm
- Tìm trên bảng số lần xuất hiện của các mặt đó.
- Tính xác suất thực nghiệm:

Tổng số lần gieo là 50.
Các mặt có số lẻ chấm của con xúc xắc là mặt 1, 3 và 5.
Số lần được mặt 1 chấm là 8 lần, mặt 3 chấm là 3 lần, mặt 5 chấm là 10 lần.
Số lần được mặt có số lẻ chấm là 8+3+10=21 lần
Xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần là:
\(\dfrac{{21}}{{50}} = 0,42\)
Khẳng định nào sau đây đúng ?
-
A.
B\(\left( 2 \right) = \left\{ {0,2,4,6,8,...} \right\}\)
-
B.
B\(\left( 2 \right) = \left\{ {0;2;4;6;8;...} \right\}\)
-
C.
B \(\left( 2 \right) = \left\{ {2;4;6;8;...} \right\}\)
-
D.
B\(\left( 2 \right) = \left\{ {1;2;4;6;8;...} \right\}\)
Đáp án : B
Ta có thể tìm các bội của một số tự nhiên \(a\) khác \(0\) bằng cách nhân số đó lần lượt với \(0,1,2,3,...\)
Ta lấy 2 nhân với số 0 thì được 0 nên 0 là bội của 2, lấy 2.1=2 nên 2 là bội của 2, 2.2=4 nên 4 là bội của 2,...
Vậy B \(\left( 2 \right) = \left\{ {0;2;4;6;8;...} \right\}\)
-
A.
Số đối của một số nguyên dương là một số nguyên âm.
-
B.
Số \(0\) không có số đối.
-
C.
Số đối của mọi số nguyên dương đều là số nguyên dương.
-
D.
Số đối của mọi số nguyên âm đều là số nguyên âm.
Đáp án : A
- Số đối của một số nguyên dương là một số nguyên âm => C sai, A đúng
- Số đối của một số nguyên âm là một số nguyên dương => D sai.
- Số đối của \(0\) là \(0\) => B sai.
Kết quả của phép trừ: \(\left( { - 47} \right) - 53\) là:
-
A.
\(6\)
-
B.
\( - 6\)
-
C.
\(100\)
-
D.
\( - 100\)
Đáp án : D
Muốn trừ số nguyên \(a\) cho số nguyên \(b\) , ta cộng \(a\) với số đối của b:
\(a - b = a + \left( { - b} \right)\)
\(\left( { - 47} \right) - 53 = - 47 + \left( { - 53} \right) = - \left( {47 + 53} \right) = - 100.\)
Viết tập hợp \(A = \left\{ {16;17;18;19} \right\}\) dưới dạng chỉ ra tính chất đặc trưng.
-
A.
\(A = \left\{ {x \in N|15 < x < 19} \right\}\)
-
B.
\(A = \left\{ {x\in N |15 < x < 20} \right\}\)
-
C.
\(A = \left\{ {x\in N |16 < x < 20} \right\}\)
-
D.
\(A = \left\{ {x\in N |15 < x \le 20} \right\}\)
Đáp án : B
+ Tìm tính chất chung của các phần tử trong tập hợp
+ Viết tập hợp dưới dạng chỉ ra tính chất đặc trưng
Nhận thấy các số \(16;17;18;19\) là các số tự nhiên lớn hơn \(15\) và nhỏ hơn \(20\)
Nên \(A = \left\{ {x \in N |15 < x < 20} \right\}\).
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là
-
A.
\(2k + 5\,\left( {k \in N} \right)\)
-
B.
\(5k + 2\,\left( {k \in N} \right)\)
-
C.
\(2k\,\left( {k \in N} \right)\)
-
D.
\(5k + 4\,\left( {k \in N} \right)\)
Đáp án : B
Số tự nhiên \(a\) chia cho \(b\) được thương \(q\) và dư $r$ có dạng \(a = b.q + r.\)
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là \(a = 5k + 2\,\left( {k \in N} \right).\)
-
A.
Hình a) và c) có trục đối xứng
-
B.
Hình c) có trục đối xứng
-
C.
Hình b) và c) có trục đối xứng
-
D.
Cả 3 hình có trục đối xứng
Đáp án : B

Ta có chữ N và Z không có trục đối xứng, chữ O có trục đối xứng.
Vậy hình c) có trục đối xứng.
 Chọn dấu thích hợp để điền vào chỗ chấm:
Chọn dấu thích hợp để điền vào chỗ chấm:
$1675 + 2468 + 325\;...\;321 + 2178 + 1822$
A. \( = \)
B. \( < \)
C. \( > \)
C. \( > \)
Áp dụng tính chất giao hoán và kết hợp của phép cộng để tính giá trị hai vế, sau đó so sánh kết quả hai vế với nhau.
Ta có:
$\begin{array}{l}1675 + 2468 + 325= (1675 + 325) + 2468 = 2000 + 2468 = 4468\,\\321 + 2178 + 1822 = 321 + (2178 + 1822) = 321 + 4000 = 4321\end{array}$
Mà \(4468 > 4321\).
Vậy $1675 + 2468 + 325\; > \;321 + 2178 + 1822$.
Gọi \(x\) là số tự nhiên thỏa mãn \({2^x} - 15 = 17\). Chọn câu đúng.
-
A.
\(x < 6\)
-
B.
\(x > 7\)
-
C.
\(x < 5\)
-
D.
\(x < 4\)
Đáp án : A
+ Tìm số bị trừ \({2^x}\) bằng cách lấy hiệu cộng với số trừ.
+ Đưa về hai lũy thừa cùng cơ số và cho hai số mũ bằng nhau.
Ta có \({2^x} - 15 = 17\)
\({2^x} = 17 + 15\)
\({2^x} = 32\)
\({2^x} = {2^5}\)
\(x = 5.\)
Vậy \(x = 5 < 6.\)
Cho \(A = 4.\left\{ {{3^2}.\left[ {\left( {{5^2} + {2^3}} \right):11} \right] - 26} \right\} + 2002\) và \(B = 134 - \left\{ {150:5 - \left[ {120:4 + 25 - \left( {12 + 18} \right)} \right]} \right\}\). Chọn câu đúng.
-
A.
$A = B$
-
B.
$A = B + 1$
-
C.
$A < B$
-
D.
$A > B$
Đáp án : D
+ Thực hiện theo thứ tự ngoặc tròn rồi ngoặc vuông rồi ngoặc nhọn.
+ Trong ngoặc ta thực hiện phép nâng lũy thừa rồi nhân chia, công trừ để tính \(A\) và \(B.\)
\(A = 4.\left\{ {{3^2}.\left[ {\left( {{5^2} + {2^3}} \right):11} \right] - 26} \right\} + 2002\)
\( = 4.\left\{ {{3^2}.\left[ {\left( {25 + 8} \right):11} \right] - 26} \right\} + 2002\)
\( = 4.\left[ {{3^2}.\left( {33:11} \right) - 26} \right] + 2002\)
\( = 4.\left( {{3^2}.3 - 26} \right) + 2002\)
\( = 4.\left( {27 - 26} \right) + 2002\)
\( = 4.1 + 2002\)
\( = 4 + 2002\)
\( = 2006.\)
Và \(B = 134 - \left\{ {150:5 - \left[ {120:4 + 25 - \left( {12 + 18} \right)} \right]} \right\}\)
\( = 134 - \left[ {150:5 - \left( {120:4 + 25 - 30} \right)} \right]\)
\( = 134 - \left[ {150:5 - \left( {30 + 25 - 30} \right)} \right]\)
\( = 134 - \left( {150:5 - 25} \right)\)
\( = 134 - \left( {30 - 25} \right)\)
\( = 134 - 5\)
\( = 129\)
Vậy \(A = 2006\) và \(B = 129\) nên \(A > B.\)
Mỗi người khi ăn thì sẽ hấp thụ ca-lo và khi hoạt động thì sẽ tiêu hao ca-lo. Bạn Bình dùng phép cộng số nguyên để tính số ca-lo hằng ngày của mình bằng cách xem số ca-lo hấp thụ là số nguyên dương và số ca-lo tiêu hao là số nguyên âm. Em hãy giúp bạn Bình kiểm tra tổng số ca-lo còn lại sau khi ăn sáng và thực hiện các hoạt động (theo số liệu trong bảng dưới đây).

-
A.
\( - 189\)
-
B.
\( 389\)
-
C.
\( - 389\)
-
D.
\( 289\)
Đáp án : B
- Tổng số ca-lo còn lại bằng ca – lo hấp thụ cộng ca- lo tiêu hao.
- Sử dụng các tính chất của phép cộng để thực hiện phép tính.
Ta có:
2 8 0 + 189 + 1 2 0 + (- 70) + (- 130)
= (2 8 0 + 1 2 0) – (70 +130) + 189
= 400 – 200 + 189
= 389 .
Vậy: Tổng số ca-lo còn lại sau khi Bình ăn sáng và thực hiện các hoạt động là 389 ca-lo.
Hình nào sau đây không có tâm đối xứng
-
A.
Hình vuông
-
B.
Hình chữ nhật
-
C.
Hình bình hành
-
D.
Hình tam giác đều
Đáp án : D
- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
- Hình tam giác đều không có tâm đối xứng.
Biểu đồ tranh dưới đây cho biết số học sinh nữ của các lớp khối 6 trường THCS Hoàng Việt.

Em hãy quan sát biểu đồ tranh ở trên và chọn đáp án đúng
-
A.
Lớp 6A1 có ít học sinh nữ nhất
-
B.
Lớp 6A4 có nhiều học sinh nữ hơn lớp 6A5
-
C.
Lớp 6A6 có 20 học sinh nữ.
-
D.
Tổng số học sinh nữ của các lớp khối 6 là 120 học sinh
Đáp án : C
Đếm số biểu tượng để tính số HS nữ của mỗi lớp (mỗi biểu tượng ứng với 10 HS nữ).
Số học sinh nữ.
Lớp 6A1: 2.10 = 20 học sinh nữ
Lớp 6A2: 3.10 = 30 học sinh nữ
Lớp 6A3: 1.10 = 10 học sinh nữ
Lớp 6A4: 2.10 = 20 học sinh nữ
Lớp 6A5: 3.10 = 30 học sinh nữ
Lớp 6A6: 2.10 = 20 học sinh nữ
Lớp 6A3 có ít học sinh nữ nhất (10 học sinh) => A sai
Lớp 6A5 có 30 học sinh nữ, lớp 6A4 có 20 học sinh nữ => Lớp 6A4 có ít học sinh nữ
hơn lớp 6A5. => B sai.
Lớp 6A6 có 20 học sinh nữ. => C đúng.
Tổng số học sinh nữ của các lớp khối 6 là: 20 + 30 + 10 + 20 + 30 + 20 = 130 học sinh.
=> D sai.
Tìm giá trị lớn nhất của biểu thức: \(C = - {\left( {x - 5} \right)^2} + 10\)
-
A.
\( - 10\)
-
B.
\(5\)
-
C.
\(0\)
-
D.
\(10\)
Đáp án : D
Áp dụng tính chất \({A^2} \ge 0\) với mọi A và tính chất \(m - {A^2} \le m\) để tìm giá trị lớn nhất của biểu thức.
\(C = - {\left( {x - 5} \right)^2} + 10\)
Ta có: \({\left( {x - 5} \right)^2} \ge 0,\,\forall x \in \mathbb{Z} \Rightarrow - {\left( {x - 5} \right)^2} \le 0,\;\,\forall x \in \mathbb{Z}\)\( \Rightarrow - {\left( {x - 5} \right)^2} + 10 \le 10,\,\;\forall x \in \mathbb{Z}\)
Suy ra \(C \le 10\,\,\forall x \in \mathbb{Z}\) .
\(C = 10\) khi \({\left( {x - 5} \right)^2} = 0 \Rightarrow x - 5 = 0 \Rightarrow x = 5\)
Vậy giá trị lớn nhất của C là 10 khi \(x = 5\) .
Toán vui. Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí nhìn khác nhau nên hai bạn thấy hai dãy các phép tính khác nhau.

Phép tính Toàn quan sát được để phép tính hai bạn quan sát thấy bằng nhau là:
-
A.
\({\bf{11}} + {\bf{8}}1 + 1{\bf{9}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{270}} \)
-
B.
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{275}} \)
-
C.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
-
D.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{6}}8 + {\bf{9}}1 + 11{\rm{ }} = {\bf{344}} \)
Đáp án : C
Điền các số: 1; 6; 8; 9 vào ô trống để được phép tính đúng.
Phép tính Toàn quan sát được là:
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
Phép tính Na quan sát được là:
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{69}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{344}} \)
Số \(A = \overline {abcd} - \left( {a + b + c + d} \right)\) chia hết cho số nào dưới đây?
-
A.
\(2\)
-
B.
\(5\)
-
C.
\(9\)
-
D.
\(6\)
Đáp án : C
+ Phân tích \(\overline {abcd} = 1000a + 100b + 10c + d\) từ đó tính được \(A.\)
+ Dựa vào tính chất chia hết của một tổng và dấu hiệu chia hết cho \(9\) để giải bài toán.
Ta có \(A = \overline {abcd} - \left( {a + b + c + d} \right)\)\( = 1000a + 100b + 10c + d - \left( {a + b + c + d} \right)\)
\( = 999a + 99b + 9c + \left( {a + b + c + d} \right) - \left( {a + b + c + d} \right)\)
\( = 999a + 99b + 9c\)
Mà \(999 \, \vdots \, 9;\,99 \, \vdots \, 9;\,9 \, \vdots \, 9\) nên \(A \, \vdots \, 9.\)
Cho hình bình hành có chu vi là 480cm, có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
-
A.
5000 cm
-
B.
10000 cm
-
C.
2500 cm 2
-
D.
5000 cm 2
Đáp án : D
- Tính nửa chu vi hình bình hành
- Tính cạnh đáy của hình bình hành
- Tính chiều cao của hình bình hành
=> Diện tích hình bình hành
Diện tích hình bình hành là: \(S = b.h\)
Trong đó \(b\) là cạnh, \(h\) là chiều cao tương ứng.
- Ta có nửa chu vi hình bình hành là: 480 : 2 = 240 (cm)
Cạnh đáy gấp 5 lần cạnh kia nên nửa chu vi sẽ gấp 6 lần cạnh kia.
- Ta có cạnh đáy hình bình hành là: 240 : 6 . 5 = 200 (cm)
- Chiều cao của hình bình hành là: 200 : 8 = 25 (cm)
- Diện tích của hình bình hành là: 200 . 25 = 5000 (cm 2 )
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
-
A.
Hai số trên có hai ước chung
-
B.
Hai số trên có ba ước chung
-
C.
Hai số trên là hai số nguyên tố cùng nhau
-
D.
Hai số trên chỉ có một ước chung là 3.
Đáp án : C
Dựa vào kiến thức 2 số nguyên tố cùng nhau là 2 số nguyên tố có ước chung lớn nhất là 1.
Áp dụng tính chất chia hết của 1 hiệu: Nếu $a \vdots c;b \vdots c \Rightarrow \left( {a - b} \right) \vdots c$
Gọi \(d = UCLN\left( {14n + 3;21n + 4} \right)\) ta có:
\(14n + 3\, \vdots \,d\) và \(21n + 4 \, \vdots \, d\)
\(3\left( {14n + 3} \right) \vdots \, d\) và \(2\left( {21n + 4} \right) \vdots d\)
\(42n + 9 \,\vdots \, d\) và \(42n + 8 \, \vdots \, d\)
\(\left( {42n + 9} \right) - \left( {42n + 8} \right) \vdots d\)
Suy ra \(1 \vdots d\)
\(d = 1\)
Vậy \(ƯCLN\left( {14n + 3;21n + 4} \right) = 1\) hay hai số đó là hai số nguyên tố cùng nhau.