Đề kiểm tra học kì 1 Toán 6 Cánh diều- Đề số 4
Đề bài
Xác định số nhỏ nhất khác 0 trong các bội chung của 2 và 3.
-
A.
0
-
B.
6
-
C.
2
-
D.
3
Tập hợp các kết quả có thể xảy ra của phép thử nghiệm tung một đồng xu là
-
A.
\(X = \left\{ {N,S} \right\}\)
-
B.
\(X = \left\{ N \right\}\)
-
C.
\(X = \left\{ S \right\}\)
-
D.
\(X = \left\{ {NN,S} \right\}\)
Giá trị của biểu thức \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\) bằng
-
A.
$140$
-
B.
$60$
-
C.
$80$
-
D.
$40$
Một hồ nước hình vuông cạnh 30 m. Tính chu vi hồ nước đó.
-
A.
120 m
-
B.
60 m
-
C.
120 dm
-
D.
900 m
-
A.
Tổng của hai số nguyên cùng dấu là một số nguyên âm.
-
B.
Tổng của hai số nguyên âm là một số nguyên âm.
-
C.
Tổng của hai số nguyên cùng dấu là một số nguyên dương.
-
D.
Tổng của hai số nguyên dương là một số nguyên âm.
-
A.
Hình con sao biển có trục đối xứng
-
B.
Hình chiếc lá có trục đối xứng
-
C.
Hai hình đều có trục đối xứng.
-
D.
Không có hình nào có trục đối xứng
Cho tổng \(M = 75 + 120 + x\) . Với giá trị nào của \(x\) dưới đây thì \(M \, \vdots \, 3?\)
-
A.
$7$
-
B.
$5$
-
C.
$4$
-
D.
$12$
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
-
A.
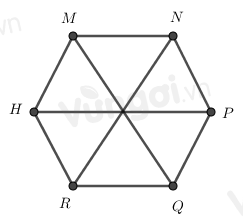
6 đỉnh là M, N, P, Q, R, H
-
B.
6 cạnh là MN, NP, PQ, MQ, QR, HM
-
C.
3 đường chéo chính là MQ, HP, RN.
-
D.
3 đường chéo chính cắt nhau tại 1 điểm.
-
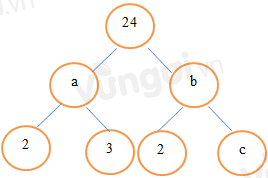
A.
$2,4,6$
-
B.
$2,6,4$
-
C.
$6,4,2$
-
D.
$6,2,4$
Viết các số tự nhiên sau bằng số La Mã: \(54;25;89;2000\)
-
A.
\(VIV;XXV;LLXXIX;ML\)
-
B.
\(LIV;XXV;LXXXIX;MM\)
-
C.
\(VIV;XXV;LXXXIX;LL\)
-
D.
\(VIV;XXV;LXXXVIIII;MM\)
+) Tích của một số chẵn các số nguyên âm là một số nguyên ..(1)..
+) Tích của một số lẻ các số nguyên âm là một số nguyên ..(2)..
Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:
-
A.
âm, dương
-
B.
dương, âm
-
C.
âm, âm
-
D.
dương, dương
Gieo một con xúc xắc 20 lần liên tiếp, có 6 lần xuất hiện mặt 3 chấm thì xác suất thực nghiệm xuất hiện mặt 3 chấm bằng
-
A.
0,15
-
B.
0,3
-
C.
0,6
-
D.
0,36

Điền số thích hợp vào chỗ trống:
Kiểm tra thị lực của một học sinh trường THCS, ta thu được bảng kết quả như sau:
|
Khối |
Số học sinh được kiểm tra |
Số học sinh bị tật khúc xạ (cận thị, viễn thị, loạn thị) |
|
6 |
210 |
14 |
|
7 |
200 |
30 |
|
8 |
180 |
40 |
|
9 |
170 |
51 |
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
-
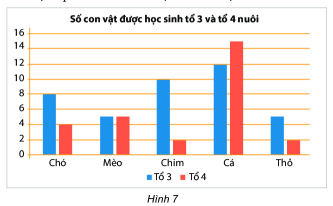
A.
Tổ 3 là 10, tổ 4 là 14
-
B.
Tổ 3 là 12, tổ 4 là 16
-
C.
Tổ 3 là 12, tổ 4 là 15
-
D.
Tổ 3 là 15, tổ 4 là 12
-
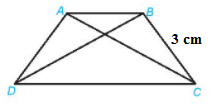
A.
AB = 3cm
-
B.
AD = 3cm
-
C.
DC = 3cm
-
D.
AC= 3cm
Viết tích \({a^4}.{a^6}\) dưới dạng một lũy thừa ta được
-
A.
\({a^8}\)
-
B.
\({a^9}\)
-
C.
\({a^{10}}\)
-
D.
\({a^2}\)
Phân số \(\dfrac{{16}}{{10}}\) được rút gọn về phân số tối giản là:
-
A.
\(\dfrac{{16}}{{10}}\)
-
B.
\(\dfrac{8}{5}\)
-
C.
2
-
D.
\(\dfrac{4}{5}\)
Tìm số tự nhiên \(n\) biết \({3^n} = 81.\)
-
A.
\(n = 2\)
-
B.
\(n = 4\)
-
C.
\(n = 5\)
-
D.
\(n = 8\)
-
A.
1,2,4
-
B.
1,2,4,6
-
C.
1,2,3,4,6,8
-
D.
1,2,4,5
Chọn câu sai
-
A.
$ - 5 < - 2$
-
B.
$0 < 4$
-
C.
$0 > - 1$
-
D.
$ - 5 < - 6$
Chọn câu trả lời đúng:
-
A.
\( - 365.366 < 1\)
-
B.
\( - 365.366 = 1\)
-
C.
\( - 365.366 = - 1\)
-
D.
\( - 365.366 > 1\)
Phát biểu nào sau đây sai ?
-
A.
Hình lục giác đều có 6 đỉnh
-
B.
Hình lục giác đều có 6 cạnh
-
C.
Hình lục giác đều có 6 đường chéo chính
-
D.
Hình lục giác đều có 6 góc
Chọn câu đúng.
-
A.
\(10000 = {10^3}\)
-
B.
\({1020^0} = 0\)
-
C.
\(x.{x^7} = {x^7}\)
-
D.
\({12^7}:{12^4} = {12^3}\)
Viết tập hợp $A = \{ x|22 < x \le 27\} $ dưới dạng liệt kê các phần tử ta được:
-
A.
\(A = \left\{ {22;23;24;25;26} \right\}\)
-
B.
\(A = \left\{ {22;23;24;25;26;27} \right\}\)
-
C.
\(A = \left\{ {23;24;25;26;27} \right\}\)
-
D.
\(A = \left\{ {23;24;25;26} \right\}\)
Tìm số tự nhiên \(x\) biết rằng \(x - 50:25 = 8.\)
-
A.
\(11\)
-
B.
\(250\)
-
C.
\(10\)
-
D.
\(20\)
Tìm các số tự nhiên \(x\) vừa chia hết cho \(2\) vừa chia hết cho \(5\) và \(1998 < x < 2018.\)
-
A.
\(x \in \left\{ {2000} \right\}\)
-
B.
\(x \in \left\{ {2000;2010} \right\}\)
-
C.
\(x \in \left\{ {2010} \right\}\)
-
D.
\(x \in \left\{ {1990;2000;2010} \right\}\)
Tìm \(x \in \mathbb{N}\), biết \(x\) chia hết cho 3 và \(360 < x < 370\)?
-
A.
$360; 366; 369$
-
B.
$363; 366; 369$
-
C.
$362; 364; 368$
-
D.
$365; 369; 366$

-
A.
\({8^o}C\)
-
B.
\( - {3^o}C\)
-
C.
\({3^o}C\)
-
D.
\({6^o}C\)
-
A.
\( - 2021;\,\, - 10;\,\,4;\,0;\, - 1\)
-
B.
\( - 2021;\,\, - 10;\,\, - 1;\,\,0;\,\,4\)
-
C.
\( - 2021;\,\, - 10;\,\,0;\,\, - 1;\,\,4\)
-
D.
\(4;\,0;\, - 1;\, - 10;\, - 2021\)
Mỗi người khi ăn thì sẽ hấp thụ ca-lo và khi hoạt động thì sẽ tiêu hao ca-lo. Bạn Bình dùng phép cộng số nguyên để tính số ca-lo hằng ngày của mình bằng cách xem số ca-lo hấp thụ là số nguyên dương và số ca-lo tiêu hao là số nguyên âm. Em hãy giúp bạn Bình kiểm tra tổng số ca-lo còn lại sau khi ăn sáng và thực hiện các hoạt động (theo số liệu trong bảng dưới đây).

-
A.
\( - 189\)
-
B.
\( 389\)
-
C.
\( - 389\)
-
D.
\( 289\)
-
A.
Hình 2
-
B.
Hình 2 và hình 3
-
C.
Hình 1, hình 2, hình 5
-
D.
Hình 1, hình 2
-
A.
96
-
B.
EF
-
C.
PQ
-
D.
Không có hình nào
Số học sinh vắng trong ngày của các lớp khối 6 trường THCS A là
|
6A1 |
6A2 |
6A3 |
6A4 |
6A5 |
6A6 |
6A7 |
6A8 |
|
2 |
4 |
5 |
1 |
3 |
2 |
2 |
1 |
Có bao nhiêu lớp có số học sinh vắng ít nhất
-
A.
4
-
B.
5
-
C.
1
-
D.
2
Biểu đồ tranh dưới đây cho biết số học sinh nữ của các lớp khối 6 trường THCS Hoàng Việt.
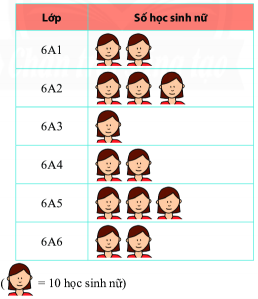
Em hãy quan sát biểu đồ tranh ở trên và chọn đáp án đúng
-
A.
Lớp 6A1 có ít học sinh nữ nhất
-
B.
Lớp 6A4 có nhiều học sinh nữ hơn lớp 6A5
-
C.
Lớp 6A6 có 20 học sinh nữ.
-
D.
Tổng số học sinh nữ của các lớp khối 6 là 120 học sinh
Toán vui. Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí nhìn khác nhau nên hai bạn thấy hai dãy các phép tính khác nhau.

Phép tính Toàn quan sát được để phép tính hai bạn quan sát thấy bằng nhau là:
-
A.
\({\bf{11}} + {\bf{8}}1 + 1{\bf{9}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{270}} \)
-
B.
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{275}} \)
-
C.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
-
D.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{6}}8 + {\bf{9}}1 + 11{\rm{ }} = {\bf{344}} \)
Tìm \(\overline {abcd} \), trong đó \(a,b,c,d\) là $4$ số tự nhiên liên tiếp tăng dần và \(\overline {abcd} \in B\left( 5 \right)\)
-
A.
$2345$
-
B.
$3210$
-
C.
$8765$
-
D.
$7890$
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
-
A.
Hai số trên có hai ước chung
-
B.
Hai số trên có ba ước chung
-
C.
Hai số trên là hai số nguyên tố cùng nhau
-
D.
Hai số trên chỉ có một ước chung là 3.
Để đánh số các trang của một quyển sách người ta phải dùng tất cả \(600\) chữ số. Hỏi quyển sách có bao nhiêu trang?
-
A.
\(326\)
-
B.
\(136\)
-
C.
\(263\)
-
D.
\(236\)
Lời giải và đáp án
Xác định số nhỏ nhất khác 0 trong các bội chung của 2 và 3.
-
A.
0
-
B.
6
-
C.
2
-
D.
3
Đáp án : B
Tìm B(2), B(3): Muốn tìm bội của một số tự nhiên ta lấy số đó nhân lần lượt với các số 0; 1; 2; 3…
Tìm BC(2,3)
Tìm số nhỏ nhất khác 0 trong các bội chung vừa tìm được.
B(2)={0;2;4;6;8;...}
B(3)={0;3;6;9;...}
Số nhỏ nhất khác 0 trong bội chung của 2 và 3 là: 6.
Tập hợp các kết quả có thể xảy ra của phép thử nghiệm tung một đồng xu là
-
A.
\(X = \left\{ {N,S} \right\}\)
-
B.
\(X = \left\{ N \right\}\)
-
C.
\(X = \left\{ S \right\}\)
-
D.
\(X = \left\{ {NN,S} \right\}\)
Đáp án : A
Liệt kê các trường hợp của phép thử nghiệm tung đồng xu.
Phép thử nghiệm tung đồng xu có kết quả có thể là sấp (S) hoặc ngửa (N).
Vậy tập hợp các kết quả có thể xảy ra là \(X = \left\{ {N,S} \right\}\)
Giá trị của biểu thức \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\) bằng
-
A.
$140$
-
B.
$60$
-
C.
$80$
-
D.
$40$
Đáp án : D
Thực hiện phép tính trong ngoặc tròn rồi đến ngoặc vuông. Sau đó là phép nhân và phép trừ.
Ta có \(2\left[ {\left( {195 + 35:7} \right):8 + 195} \right] - 400\)
\( = 2\left[ {\left( {195 + 5} \right):8 + 195} \right] - 400\)
\( = 2\left[ {200:8 + 195} \right] - 400\)
\( = 2\left( {25 + 195} \right) - 400\)
\( = 2.220 - 400\)
\( = 440 - 400\)
\( = 40\)
Một hồ nước hình vuông cạnh 30 m. Tính chu vi hồ nước đó.
-
A.
120 m
-
B.
60 m
-
C.
120 dm
-
D.
900 m
Đáp án : A
Muốn tính chu vi hình vuông ta lấy độ dài một cạnh nhân với 4.
Chu vi hồ nước là:
30 . 4 = 120 (m)
-
A.
Tổng của hai số nguyên cùng dấu là một số nguyên âm.
-
B.
Tổng của hai số nguyên âm là một số nguyên âm.
-
C.
Tổng của hai số nguyên cùng dấu là một số nguyên dương.
-
D.
Tổng của hai số nguyên dương là một số nguyên âm.
Đáp án : B
A và C sai do tổng của hai số nguyên cùng dấu có thể là số nguyên âm có thể là số nguyên dương
D sai vì tổng của hai số nguyên dương là một số nguyên dương
B đúng
-
A.
Hình con sao biển có trục đối xứng
-
B.
Hình chiếc lá có trục đối xứng
-
C.
Hai hình đều có trục đối xứng.
-
D.
Không có hình nào có trục đối xứng
Đáp án : A

Vậy hình con sao biển có trục đối xứng.
Cho tổng \(M = 75 + 120 + x\) . Với giá trị nào của \(x\) dưới đây thì \(M \, \vdots \, 3?\)
-
A.
$7$
-
B.
$5$
-
C.
$4$
-
D.
$12$
Đáp án : D
Sử dụng tính chất 1: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó. \(a\, \vdots \,m;\,b\, \vdots \,m;\,c\, \vdots \,m \Rightarrow \left( {a + b + c} \right) \vdots \,m\)
Vì \(75\, \vdots \,3;\,120\, \vdots \,3\) nên để \(M = 75 + 120 + x\) chia hết cho \(3\) thì \(x\, \vdots \,3\) nên ta chọn \(x = 12.\)
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
Đáp án : A
- Áp dụng kiến thức:
Mọi số tự nhiên đều có ước là $1$.
Số nguyên tố có $2$ ước là $1$ và chính nó.
Mọi số nguyên tố khác nhau đều có ước chung duy nhất là $1$.
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$.
B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.
C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.
D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.
-
A.
6 đỉnh là M, N, P, Q, R, H
-
B.
6 cạnh là MN, NP, PQ, MQ, QR, HM
-
C.
3 đường chéo chính là MQ, HP, RN.
-
D.
3 đường chéo chính cắt nhau tại 1 điểm.
Đáp án : B
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Đáp án B sai do MQ là đường chéo chính, sửa lại:
6 cạnh là MN, NP, PQ, HR, QR, HM
-
A.
$2,4,6$
-
B.
$2,6,4$
-
C.
$6,4,2$
-
D.
$6,2,4$
Đáp án : C
$a=2.3=6$
$6.b=24=>b=4$
$2.c=b=>c=4:2=2$
Vậy $a=6,b=4,c=2$.
Viết các số tự nhiên sau bằng số La Mã: \(54;25;89;2000\)
-
A.
\(VIV;XXV;LLXXIX;ML\)
-
B.
\(LIV;XXV;LXXXIX;MM\)
-
C.
\(VIV;XXV;LXXXIX;LL\)
-
D.
\(VIV;XXV;LXXXVIIII;MM\)
Đáp án : B
+ Vì \(50 = L;4 = IV\) nên \(54 = LIV\)
+ Vì \(10 = X;V = 5\) nên \(25 = XXV\)
+ \(89 = 50 + 10 + 10 + 10 + 9 = LXXXIX\)
+ \(2000 = 1000 + 1000 = MM\)
+) Tích của một số chẵn các số nguyên âm là một số nguyên ..(1)..
+) Tích của một số lẻ các số nguyên âm là một số nguyên ..(2)..
Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:
-
A.
âm, dương
-
B.
dương, âm
-
C.
âm, âm
-
D.
dương, dương
Đáp án : B
- Tích của hai số nguyên trái dấu là số nguyên âm.
- Tính của hai số nguyên cùng dấu là số nguyên dương.
+) Tích của một số chẵn các số nguyên âm là một số nguyên dương
+) Tích của một số lẻ các số nguyên âm là một số nguyên âm
Gieo một con xúc xắc 20 lần liên tiếp, có 6 lần xuất hiện mặt 3 chấm thì xác suất thực nghiệm xuất hiện mặt 3 chấm bằng
-
A.
0,15
-
B.
0,3
-
C.
0,6
-
D.
0,36
Đáp án : B
- Xác định số lần xuất hiện mặt 3 chấm.
- Xác suất thực nghiệm=Số lần xuất hiện mặt 3 chấm: Tổng số lần gieo
Tổng số lần gieo là 20, số lần xuất hiện mặt 3 chấm là 6 lần.
Xác suất thực nghiệm xuất hiện mặt 3 chấm bằng \(\dfrac{6}{{20}} = 0,3\).

Điền số thích hợp vào chỗ trống:
Kiểm tra thị lực của một học sinh trường THCS, ta thu được bảng kết quả như sau:
|
Khối |
Số học sinh được kiểm tra |
Số học sinh bị tật khúc xạ (cận thị, viễn thị, loạn thị) |
|
6 |
210 |
14 |
|
7 |
200 |
30 |
|
8 |
180 |
40 |
|
9 |
170 |
51 |
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là
, khối 7 là
, khối 8 là
, khối 9 là
Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối
- Tính xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” từng khối.
Xác suất thực nghiệm=Số học sinh bị khúc xạ: Số học sinh được kiểm tra.
- So sánh các phân số với nhau.
Số học sinh bị khúc xạ khối 6 là 14. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 6 là \(\dfrac{{14}}{{210}} = \dfrac{1}{{15}}\)
Số học sinh bị khúc xạ khối 7 là 30. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 7 là \(\dfrac{{30}}{{200}} = \dfrac{3}{{20}}\)
Số học sinh bị khúc xạ khối 8 là 40. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 8 là \(\dfrac{{40}}{{180}} = \dfrac{2}{9}\)
Số học sinh bị khúc xạ khối 9 là 51. Xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” khối 9 là \(\dfrac{{51}}{{170}} = \dfrac{3}{{10}}\)
Số lớn nhất trong các số \(\dfrac{1}{{15}};\dfrac{3}{{20}};\dfrac{2}{9};\dfrac{3}{{10}}\) là \(\dfrac{3}{{10}}\).
Vậy khối có xác suất thực nghiệm của sự kiện “học sinh bị khúc xạ” lớn nhất là khối 9
Chọn phát biểu sai ?
-
A.
Hình có bốn đỉnh là hình chữ nhật
-
B.
Hình chữ nhật có bốn đỉnh
-
C.
Hình chữ nhật có hai cặp cạnh đối song song.
-
D.
Hình chữ nhật có hai đường chéo bằng nhau
Đáp án : A
Sử dụng dấu hiệu nhận biết hình chữ nhật
Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.
=> Đáp án B, C, D đúng.
Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ:
-
A.
Tổ 3 là 10, tổ 4 là 14
-
B.
Tổ 3 là 12, tổ 4 là 16
-
C.
Tổ 3 là 12, tổ 4 là 15
-
D.
Tổ 3 là 15, tổ 4 là 12
Đáp án : C
- Tổ 3: Màu xanh
- Tổ 4: Màu đỏ
Số cá tổ 3: 12
Số cá tổ 4: 15
-
A.
AB = 3cm
-
B.
AD = 3cm
-
C.
DC = 3cm
-
D.
AC= 3cm
Đáp án : B
Hình thang cân có hai cạnh bên bằng nhau.
Hình thang cân ABCD có AD và BC là hai cạnh bên nên: AD = BC = 3 cm.
Viết tích \({a^4}.{a^6}\) dưới dạng một lũy thừa ta được
-
A.
\({a^8}\)
-
B.
\({a^9}\)
-
C.
\({a^{10}}\)
-
D.
\({a^2}\)
Đáp án : C
Sử dụng công thức nhân hai lũy thừa cùng cơ số ${a^m}.{a^n} = {a^{m + n}}$
Ta có \({a^4}.{a^6}\)\( = {a^{4 + 6}} = {a^{10}}\)
Phân số \(\dfrac{{16}}{{10}}\) được rút gọn về phân số tối giản là:
-
A.
\(\dfrac{{16}}{{10}}\)
-
B.
\(\dfrac{8}{5}\)
-
C.
2
-
D.
\(\dfrac{4}{5}\)
Đáp án : B
Nếu tử và mẫu của phân số đã cho có ước chung thì phân số chưa tối giản, nếu không có ước chung thì phân số đã tối giản.
Tìm ước chung hoặc ước chung lớn nhất của tử số và mẫu số.
ƯC(15, 10)=2. Ta chia cả tử và mẫu của \(\dfrac{{16}}{{10}}\) cho \(2\) được:
\(\dfrac{{16}}{{10}} = \dfrac{{16:2}}{{10:2}} = \dfrac{8}{5}\).
Tìm số tự nhiên \(n\) biết \({3^n} = 81.\)
-
A.
\(n = 2\)
-
B.
\(n = 4\)
-
C.
\(n = 5\)
-
D.
\(n = 8\)
Đáp án : B
Đưa hai vế về hai lũy thừa cùng số mũ rồi sử dụng \({a^n} = {a^m}\left( {a \ne 0;a \ne 1} \right)\) thì \(n = m.\)
Ta có \({3^n} = 81\) mà \(81 = {3^4}\) nên \({3^n} = {3^4}\) suy ra \(n = 4.\)
-
A.
1,2,4
-
B.
1,2,4,6
-
C.
1,2,3,4,6,8
-
D.
1,2,4,5
Đáp án : C

Vậy hình 1,2,3,4,6,8 là các hình có trục đối xứng.
Chọn câu sai
-
A.
$ - 5 < - 2$
-
B.
$0 < 4$
-
C.
$0 > - 1$
-
D.
$ - 5 < - 6$
Đáp án : D
Khi biểu diễn trên trục số ( nằm ngang ):
+ Điểm $a$ nằm bên trái điểm $b$ thì số nguyên $a$ nhỏ hơn số nguyên $b.$
+ Điểm $a$ nằm bên phải điểm $b$ thì số nguyên $a$ lớn hơn số nguyên $b.$
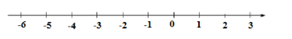
Điểm $ - 5$ nằm bên trái điểm $ - 2$ nên $ - 5 < - 2.$ Do đó A đúng.
Điểm $0$ nằm bên trái điểm $4$ nên $0 < 4.$ Do đó B đúng.
Điểm $0$ nằm bên phải điểm $ - 1$ nên $0 > - 1.$ Do đó C đúng.
Điểm $ - 5$ nằm bên phải điểm $ - 6$ nên $ - 5 > - 6$ Do đó D sai.
Chọn câu trả lời đúng:
-
A.
\( - 365.366 < 1\)
-
B.
\( - 365.366 = 1\)
-
C.
\( - 365.366 = - 1\)
-
D.
\( - 365.366 > 1\)
Đáp án : A
Áp dụng quy tắc nhân hai số nguyên khác dấu: Khi nhân hai số nguyên khác dấu ta được một số âm
Áp dụng quy tắc nhân hai số nguyên khác dấu ta có:
\( - 365.366 < 0 < 1\) và \( - 365.366 \ne - 1\)
Phát biểu nào sau đây sai ?
-
A.
Hình lục giác đều có 6 đỉnh
-
B.
Hình lục giác đều có 6 cạnh
-
C.
Hình lục giác đều có 6 đường chéo chính
-
D.
Hình lục giác đều có 6 góc
Đáp án : C
Sử dụng dấu hiệu nhận biết lục giác đều.
Các đáp án A, B, D đúng.
Hình lục giác đều có 3 đường chéo chính => Đáp án C sai .
Chọn câu đúng.
-
A.
\(10000 = {10^3}\)
-
B.
\({1020^0} = 0\)
-
C.
\(x.{x^7} = {x^7}\)
-
D.
\({12^7}:{12^4} = {12^3}\)
Đáp án : D
Dựa vào quy tắc nhân, chia hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\,\,\,\left( {m;n \in N} \right);\)\(\,\,{a^m}:{a^n} = {a^{m - n}}\,\,\,\left( {a \ne 0;m \ge n} \right)\)
Ta có:
\(\begin{array}{l}10000 = {10^4}\\{1020^0} = 1\\x.{x^7} = {x^{1 + 7}} = {x^8}\\{12^7}:{12^4} = {12^{7 - 4}} = {12^3}\end{array}\)
Do đó chỉ có đáp án D đúng.
Viết tập hợp $A = \{ x|22 < x \le 27\} $ dưới dạng liệt kê các phần tử ta được:
-
A.
\(A = \left\{ {22;23;24;25;26} \right\}\)
-
B.
\(A = \left\{ {22;23;24;25;26;27} \right\}\)
-
C.
\(A = \left\{ {23;24;25;26;27} \right\}\)
-
D.
\(A = \left\{ {23;24;25;26} \right\}\)
Đáp án : C
+ Chỉ ra các số lớn hơn \(22\) và nhỏ hơn hoặc bằng \(27.\)
+ Từ đó viết tập hợp A dưới dạng liệt kê.
Các số lớn hơn \(22\) và nhỏ hơn hoặc bằng \(27\) là \(23;24;25;26;27.\)
Nên \(A = \left\{ {23;24;25;26;27} \right\}.\)
Tìm số tự nhiên \(x\) biết rằng \(x - 50:25 = 8.\)
-
A.
\(11\)
-
B.
\(250\)
-
C.
\(10\)
-
D.
\(20\)
Đáp án : C
Thực hiện phép chia trước rồi tìm \(x\) bằng cách lấy hiệu cộng với số trừ.
Ta có \(x - 50:25 = 8\)
\(x - 2 = 8\)
\(x = 8 + 2\)
\(x = 10.\)
Tìm các số tự nhiên \(x\) vừa chia hết cho \(2\) vừa chia hết cho \(5\) và \(1998 < x < 2018.\)
-
A.
\(x \in \left\{ {2000} \right\}\)
-
B.
\(x \in \left\{ {2000;2010} \right\}\)
-
C.
\(x \in \left\{ {2010} \right\}\)
-
D.
\(x \in \left\{ {1990;2000;2010} \right\}\)
Đáp án : B
Sử dụng: Các số tự nhiên vừa chia hết cho \(2\) vừa chia hết cho \(5\) có chữ số tận cùng là \(0.\)
Vì \(x \, \vdots \, 2;\,x \, \vdots \, 5\) nên \(x\) có chữ số tận cùng là \(0\) và \(1998 < x < 2018\) suy ra \(x = 2000;x = 2010.\)
Tìm \(x \in \mathbb{N}\), biết \(x\) chia hết cho 3 và \(360 < x < 370\)?
-
A.
$360; 366; 369$
-
B.
$363; 366; 369$
-
C.
$362; 364; 368$
-
D.
$365; 369; 366$
Đáp án : B
\(360 < x < 370\) : Các số từ 361 đến 369.
Sử dụng lý thuyết và dấu hiệu chia hết cho 3 và tìm các số từ 361 đến 369 chia hết cho 3
\(360 < x < 370\) : Các số từ 361 đến 369. Đó là 361; 362; 363; 364; 365; 366; 367; 368; 369
Trong các số trên chỉ có số 363; 366; 369 là chia hết cho 3 (Tính tổng các chữ số).

-
A.
\({8^o}C\)
-
B.
\( - {3^o}C\)
-
C.
\({3^o}C\)
-
D.
\({6^o}C\)
Đáp án : B
Hai vạch liên tiếp của nhiệt kế cách nhau 1 đơn vị.
Coi nhiệt kế như trục số thẳng đứng, chiều dương từ dưới lên trên.
-
A.
\( - 2021;\,\, - 10;\,\,4;\,0;\, - 1\)
-
B.
\( - 2021;\,\, - 10;\,\, - 1;\,\,0;\,\,4\)
-
C.
\( - 2021;\,\, - 10;\,\,0;\,\, - 1;\,\,4\)
-
D.
\(4;\,0;\, - 1;\, - 10;\, - 2021\)
Đáp án : B
- So sánh các số
- Sắp xếp các số nguyên theo thứ tự tăng dần tức là số nào nhỏ hơn ta viết trước, số lớn hơn ta viết sau.
Ta có: \( - 2021 < \, - 10 < \, - 1 < \,\,0 < \,\,4\).
Sắp xếp theo thứ tự tăng dần: \( - 2021;\,\, - 10;\,\, - 1;\,\,0;\,\,4\)
Mỗi người khi ăn thì sẽ hấp thụ ca-lo và khi hoạt động thì sẽ tiêu hao ca-lo. Bạn Bình dùng phép cộng số nguyên để tính số ca-lo hằng ngày của mình bằng cách xem số ca-lo hấp thụ là số nguyên dương và số ca-lo tiêu hao là số nguyên âm. Em hãy giúp bạn Bình kiểm tra tổng số ca-lo còn lại sau khi ăn sáng và thực hiện các hoạt động (theo số liệu trong bảng dưới đây).

-
A.
\( - 189\)
-
B.
\( 389\)
-
C.
\( - 389\)
-
D.
\( 289\)
Đáp án : B
- Tổng số ca-lo còn lại bằng ca – lo hấp thụ cộng ca- lo tiêu hao.
- Sử dụng các tính chất của phép cộng để thực hiện phép tính.
Ta có:
2 8 0 + 189 + 1 2 0 + (- 70) + (- 130)
= (2 8 0 + 1 2 0) – (70 +130) + 189
= 400 – 200 + 189
= 389 .
Vậy: Tổng số ca-lo còn lại sau khi Bình ăn sáng và thực hiện các hoạt động là 389 ca-lo.
-
A.
Hình 2
-
B.
Hình 2 và hình 3
-
C.
Hình 1, hình 2, hình 5
-
D.
Hình 1, hình 2
Đáp án : C
Hình bình hành là tứ giác có hai cặp cạnh đối diện song song và bằng nhau.
Do hình bình hành là tứ giác có hai cặp cạnh đối diện song song và bằng nhau.
=> Các hình là hình bình hành là: Hình 1, hình 2, hình 5.
-
A.
96
-
B.
EF
-
C.
PQ
-
D.
Không có hình nào
Đáp án : A
Hình có tâm đối xứng là:

Số học sinh vắng trong ngày của các lớp khối 6 trường THCS A là
|
6A1 |
6A2 |
6A3 |
6A4 |
6A5 |
6A6 |
6A7 |
6A8 |
|
2 |
4 |
5 |
1 |
3 |
2 |
2 |
1 |
Có bao nhiêu lớp có số học sinh vắng ít nhất
-
A.
4
-
B.
5
-
C.
1
-
D.
2
Đáp án : D
- Tìm số bé nhất trong hàng thứ hai
- Tìm số lớp có số lượng học sinh vắng vừa tìm được.
Số học sinh vắng ít nhất trong một lớp là 1
Lớp có số học sinh vắng ít nhất là lớp 6A4 , 6A8
Vậy có 2 lớp có số học sinh vắng ít nhất.
Biểu đồ tranh dưới đây cho biết số học sinh nữ của các lớp khối 6 trường THCS Hoàng Việt.

Em hãy quan sát biểu đồ tranh ở trên và chọn đáp án đúng
-
A.
Lớp 6A1 có ít học sinh nữ nhất
-
B.
Lớp 6A4 có nhiều học sinh nữ hơn lớp 6A5
-
C.
Lớp 6A6 có 20 học sinh nữ.
-
D.
Tổng số học sinh nữ của các lớp khối 6 là 120 học sinh
Đáp án : C
Đếm số biểu tượng để tính số HS nữ của mỗi lớp (mỗi biểu tượng ứng với 10 HS nữ).
Số học sinh nữ.
Lớp 6A1: 2.10 = 20 học sinh nữ
Lớp 6A2: 3.10 = 30 học sinh nữ
Lớp 6A3: 1.10 = 10 học sinh nữ
Lớp 6A4: 2.10 = 20 học sinh nữ
Lớp 6A5: 3.10 = 30 học sinh nữ
Lớp 6A6: 2.10 = 20 học sinh nữ
Lớp 6A3 có ít học sinh nữ nhất (10 học sinh) => A sai
Lớp 6A5 có 30 học sinh nữ, lớp 6A4 có 20 học sinh nữ => Lớp 6A4 có ít học sinh nữ
hơn lớp 6A5. => B sai.
Lớp 6A6 có 20 học sinh nữ. => C đúng.
Tổng số học sinh nữ của các lớp khối 6 là: 20 + 30 + 10 + 20 + 30 + 20 = 130 học sinh.
=> D sai.
Toán vui. Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí nhìn khác nhau nên hai bạn thấy hai dãy các phép tính khác nhau.

Phép tính Toàn quan sát được để phép tính hai bạn quan sát thấy bằng nhau là:
-
A.
\({\bf{11}} + {\bf{8}}1 + 1{\bf{9}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{270}} \)
-
B.
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{275}} \)
-
C.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
-
D.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{6}}8 + {\bf{9}}1 + 11{\rm{ }} = {\bf{344}} \)
Đáp án : C
Điền các số: 1; 6; 8; 9 vào ô trống để được phép tính đúng.
Phép tính Toàn quan sát được là:
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
Phép tính Na quan sát được là:
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{69}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{344}} \)
Tìm \(\overline {abcd} \), trong đó \(a,b,c,d\) là $4$ số tự nhiên liên tiếp tăng dần và \(\overline {abcd} \in B\left( 5 \right)\)
-
A.
$2345$
-
B.
$3210$
-
C.
$8765$
-
D.
$7890$
Đáp án : A
+) Dùng tính chất của bội.
+) Sử dụng dấu hiệu chia hết của các số $5$ và $9.$
$\overline {abcd} \in B\left( 5 \right)$
Ta có:
$\overline {abcd} \in B\left( 5 \right) \Rightarrow \overline {abcd} \vdots 5 \Rightarrow d \in \left\{ {0;5} \right\}$
$d = 5 \Rightarrow \overline {abcd} = 2345$
\({\rm{d}} = 0 \Rightarrow \) Loại, vì $a,b,c,d$ là $4$ số tự nhiên liên tiếp tăng dần.
Vậy $\overline {abcd} = 2345.$
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
-
A.
Hai số trên có hai ước chung
-
B.
Hai số trên có ba ước chung
-
C.
Hai số trên là hai số nguyên tố cùng nhau
-
D.
Hai số trên chỉ có một ước chung là 3.
Đáp án : C
Dựa vào kiến thức 2 số nguyên tố cùng nhau là 2 số nguyên tố có ước chung lớn nhất là 1.
Áp dụng tính chất chia hết của 1 hiệu: Nếu $a \vdots c;b \vdots c \Rightarrow \left( {a - b} \right) \vdots c$
Gọi \(d = UCLN\left( {14n + 3;21n + 4} \right)\) ta có:
\(14n + 3\, \vdots \,d\) và \(21n + 4 \, \vdots \, d\)
\(3\left( {14n + 3} \right) \vdots \, d\) và \(2\left( {21n + 4} \right) \vdots d\)
\(42n + 9 \,\vdots \, d\) và \(42n + 8 \, \vdots \, d\)
\(\left( {42n + 9} \right) - \left( {42n + 8} \right) \vdots d\)
Suy ra \(1 \vdots d\)
\(d = 1\)
Vậy \(ƯCLN\left( {14n + 3;21n + 4} \right) = 1\) hay hai số đó là hai số nguyên tố cùng nhau.
Để đánh số các trang của một quyển sách người ta phải dùng tất cả \(600\) chữ số. Hỏi quyển sách có bao nhiêu trang?
-
A.
\(326\)
-
B.
\(136\)
-
C.
\(263\)
-
D.
\(236\)
Đáp án : D
Chia ra thành các trang đánh \(1\) chữ số; \(2\) chữ số và \(3\) chữ số để tìm số trang của quyển sách.
\(99\) trang đầu cần dùng \(9.1 + 90.2 = 189\) chữ số
\(999\) trang đầu cần dùng \(9.1 + 90.2 + 900.3 = 2889\) chữ số
Vì \(189 < 600 < 2889\) nên trang cuối cùng phải có ba chữ số
Số chữ số dùng để đánh số trang có ba chữ số là \(600 - 189 = 411\) (chữ số)
Số trang có ba chữ số là \(411:3 = 137\) trang
Số trang của quyển sách là \(99 + 137 = 236\) trang