Đề kiểm tra giữa học kì 1 Toán 6 Cánh diều - Đề số 2
Đề bài
Số nào trong các số sau là ước nguyên tố của 52?
-
A.
26
-
B.
3
-
C.
13
-
D.
1
Cách viết tập hợp nào sau đây là đúng?
-
A.
\(A = \left[ {0;1;2;3} \right]\)
-
B.
\(A = \left( {0;1;2;3} \right)\)
-
C.
\(A = 1;2;3\)
-
D.
\(A = \left\{ {0;1;2;3} \right\}\)
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
-
A.
\(x\)
-
B.
\(6\)
-
C.
\(3\)
-
D.
\(18\)
\({2^3}.16\) bằng
-
A.
\({2^7}\)
-
B.
\({2^8}\)
-
C.
\({2^9}\)
-
D.
\({2^{12}}\)
Cho ${a^2}.b.7 = 140$ với \(a,b\) là các số nguyên tố, vậy \(a\) có giá trị là bao nhiêu:
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Trong các số $333; 354; 360; 2457; 1617; 152,$ các số chia hết cho $9$ là
-
A.
$333$
-
B.
$360$
-
C.
$2457$
-
D.
Cả A, B, C đều đúng
Số liền trước số \(1000\) là
-
A.
\(1002\)
-
B.
\(990\)
-
C.
\(1001\)
-
D.
\(999\)
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
 Bình nói: “\(a + b = b + a\)”. Đúng hay sai?
Bình nói: “\(a + b = b + a\)”. Đúng hay sai?
Tập hợp số tự nhiên được kí hiệu là
-
A.
\(N\)
-
B.
\({N^*}\)
-
C.
\(\left\{ N \right\}\)
-
D.
\(Z\)
Cho \(A = 90.17 + 34.40 + 12.51\) và \(B = 5.7.9 + 2.5.6\) . Chọn câu đúng.
-
A.
A là số nguyên tố, B là hợp số
-
B.
A là hợp số, B là số nguyên tố
-
C.
Cả A và B là số nguyên tố
-
D.
Cả A và B đều là hợp số
-
A.
Hình con sao biển có trục đối xứng
-
B.
Hình chiếc lá có trục đối xứng
-
C.
Hai hình đều có trục đối xứng.
-
D.
Không có hình nào có trục đối xứng
Lớp 6A có 45 học sinh, có thể chia lớp thành hai nhóm, mỗi nhóm có số lượng học sinh bằng nhau.
-
A.
\(MQ = NR\)
-
B.
\(MH = RQ\)
-
C.
\(MN = HR\)
-
D.
\(MH = MQ\)
Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
-
A.
0, 1, 2, 3
-
B.
0, 2, 4, 6, 8
-
C.
1, 3, 5, 7, 9
-
D.
0 hoặc 5
Chọn câu đúng.
-
A.
\({5^2}{.5^3}{.5^4} = {5^{10}}\)
-
B.
\({5^2}{.5^3}:{5^4} = 5\)
-
C.
\({5^3}:5 = 5\)
-
D.
\({5^1} = 1\)
$BCNN(9;24)$ là bao nhiêu?
-
A.
$54$
-
B.
$18$
-
C.
$72$
-
D.
$36$
-
A.
\(AB = AC\)
-
B.
\(AC = DO\)
-
C.
\(AC = BD\)
-
D.
\(OB = AC\)
Tìm số tự nhiên $x$ thỏa mãn: $7+x=362$.
-
A.
300
-
B.
355
-
C.
305
-
D.
362
Cho các số \(21;77;71;101\). Chọn câu đúng.
-
A.
Số \(21\) là hợp số, các số còn lại là số nguyên tố
-
B.
Có hai số nguyên tố và hai hợp số trong các số trên.
-
C.
Chỉ có một số nguyên tố còn lại là hợp số
-
D.
Không có số nguyên tố nào trong các số trên
Khẳng định nào sau đây đúng ?
-
A.
B\(\left( 2 \right) = \left\{ {0,2,4,6,8,...} \right\}\)
-
B.
B\(\left( 2 \right) = \left\{ {0;2;4;6;8;...} \right\}\)
-
C.
B \(\left( 2 \right) = \left\{ {2;4;6;8;...} \right\}\)
-
D.
B\(\left( 2 \right) = \left\{ {1;2;4;6;8;...} \right\}\)
Chọn câu đúng:
-
A.
Chu vi của một hình bình hành bằng tổng một cặp cạnh kề nhau bất kỳ.
-
B.
Chu vi hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Chu vi hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
-
A.
\(49\,cm\)
-
B.
\(49\,\,c{m^2}\)
-
C.
\(98\,\,c{m^2}\)
-
D.
\(98\,\,cm\)
Sau khi phân tích 45, 150 ra các thừa số nguyên tố được 45 = 3 2 .5 và 150 = 2.3.5 2 . Số mũ nhỏ nhất của thừa số chung 3 là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Cho \(B = \left\{ {2;3;4;5} \right\}\). Chọn câu sai.
-
A.
\(2 \in B\)
-
B.
\(5 \in B\)
-
C.
\(1 \notin B\)
-
D.
\(6 \in B\)
Cho tam giác ABC có độ dài cạnh AB bằng 12 cm.Tổng độ dài hai cạnh BC và CA hơn độ dài cạnh AB là 7cm, chu vi tam giác ABC bằng:
-
A.
19 cm
-
B.
31 cm
-
C.
17 cm
-
D.
31 dm
Tổng \(1 + 2 + 3 + 4 + ... + 2018\) bằng
-
A.
\(4074342\)
-
B.
\(2037171\)
-
C.
\(2036162\)
-
D.
\(2035152\)
Có bao nhiêu số vừa là bội của $5$ vừa là ước của $50$?
-
A.
$4$ số
-
B.
$5$ số
-
C.
$6$ số
-
D.
$7$ số
Tìm số tự nhiên \(\overline {145*} \) chia hết cho cả \(3\) và \(5.\)
-
A.
\(1454\)
-
B.
\(1450\)
-
C.
\(1455\)
-
D.
\(1452\)
Nếu cho 7 hình vuông đơn vị ghép thành hình chữ nhật thì có mấy cách xếp (Không kể việc xoay chiều dài và chiều rộng)?
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Tìm tất cả các số tự nhiên \(n\) để \({n^2} + 12n\) là số nguyên tố.
-
A.
$n = 11$
-
B.
$n = 13$
-
C.
$n = 2$
-
D.
$n = 1$
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ \(800\) đến \(900\) em.
-
A.
$845$
-
B.
$840$
-
C.
$860$
-
D.
$900$
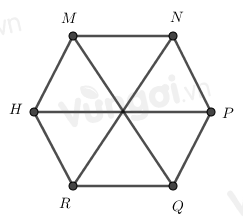
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
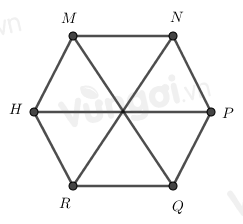
-
A.
8
-
B.
2
-
C.
4
-
D.
6
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
-
A.
110 cm 2
-
B.
112 cm 2
-
C.
111 cm 2
-
D.
114 cm 2
-
A.
Tam giác đều, trái tim, cánh diều
-
B.
Cánh quạt, trái tim, cánh diều
-
C.
Trái tim, Cánh diều
-
D.
Cả bốn hình
Tìm số tự nhiên n lớn nhất có $3$ chữ số sao cho $n$ chia $8$ dư $7,$ chia $31$ dư $28.$
-
A.
$927$
-
B.
$183$
-
C.
$431$
-
D.
$729$
Cho \(P = 1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}\). Chọn đáp án đúng.
-
A.
\(123.P = {5^{102}} - 1\)
-
B.
\(124.P = {5^{102}} - 1\)
-
C.
\(124.P = {5^{101}} - 1\)
-
D.
\(124.P = {5^{102}}\)
Sân trường em hình vuông. Để tăng thêm diện tích nhà trường mở rộng về mỗi phía 4m thì diện tích tăng thêm 192m 2 . Hỏi trước đây sân trường em có diện tích là bao nhiêu m 2 ?
-
A.
16 m 2
-
B.
32 m 2
-
C.
64 m 2
-
D.
128 m 2
Toán vui. Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí nhìn khác nhau nên hai bạn thấy hai dãy các phép tính khác nhau.

Phép tính Toàn quan sát được để phép tính hai bạn quan sát thấy bằng nhau là:
-
A.
\({\bf{11}} + {\bf{8}}1 + 1{\bf{9}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{270}} \)
-
B.
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{275}} \)
-
C.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
-
D.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{6}}8 + {\bf{9}}1 + 11{\rm{ }} = {\bf{344}} \)
Lời giải và đáp án
Số nào trong các số sau là ước nguyên tố của 52?
-
A.
26
-
B.
3
-
C.
13
-
D.
1
Đáp án : C
Xét từng đáp án.
Loại các đáp án không là số nguyên tố hoặc không là ước của 52.
Ta thấy 26 và 1 đều là các ước của 52 nhưng không là số nguyên tố.
số 3 là số nguyên tố nhưng không là ước của 52 nên loại A.
13 là một ước của 52 và 13 là một số nguyên tố nên 13 là ước nguyên tố của 52.
Cách viết tập hợp nào sau đây là đúng?
-
A.
\(A = \left[ {0;1;2;3} \right]\)
-
B.
\(A = \left( {0;1;2;3} \right)\)
-
C.
\(A = 1;2;3\)
-
D.
\(A = \left\{ {0;1;2;3} \right\}\)
Đáp án : D
Sử dụng cách viết tập hợp
+ Tên tập hợp được viết bằng các chữ cái in hoa như A ; B ; C ;...
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ” (nếu có phần tử số)
Cách viết đúng là \(A = \left\{ {0;1;2;3} \right\}.\)
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
-
A.
\(x\)
-
B.
\(6\)
-
C.
\(3\)
-
D.
\(18\)
Đáp án : B
Ta sử dụng (số bị chia) : (số chia) = (thương) để xác định thương của phép chia
Phép chia \(x:3 = 6\) có \(x\) là số bị chia; \(3\) là số chia và \(6\) là thương.
Nên thương của phép chia là \(6.\)
\({2^3}.16\) bằng
-
A.
\({2^7}\)
-
B.
\({2^8}\)
-
C.
\({2^9}\)
-
D.
\({2^{12}}\)
Đáp án : A
Chuyển 16 thành lũy thừa cơ số 2: Tách 16 thành tích của các thừa số 2.
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
\({a^m}.{a^n} = {a^{m + n}}\)
\(\begin{array}{l}16 = 2.2.2.2 = {2^4}\\{2^3}.16 = {2^3}{.2^4} = {2^{3 + 4}} = {2^7}\end{array}\)
Cho ${a^2}.b.7 = 140$ với \(a,b\) là các số nguyên tố, vậy \(a\) có giá trị là bao nhiêu:
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Đáp án : B
- Phân tích số \(140\) thành tích các thừa số nguyên tố.

Suy ra $140 = {2^2}.5.7 = {a^2}.b.7$ nên \(a = 2\).
Trong các số $333; 354; 360; 2457; 1617; 152,$ các số chia hết cho $9$ là
-
A.
$333$
-
B.
$360$
-
C.
$2457$
-
D.
Cả A, B, C đều đúng
Đáp án : D
Sử dụng dấu hiệu chia hết cho $9$ : Các số có tổng các chữ số chia hết cho $9$ thì chia hết cho $9.$
Các số $333;2457;360$ là các số chia hết cho $9$ vì tổng các chữ số của nó chia hết cho $9.$
+) Số $333$ có tổng các chữ số là $3+3+3=9 \, \vdots \, 9$ nên $ 333 \, \vdots \, 9.$
+) Số $2457$ có tổng các chữ số là $2+4+5+7=18 \, \vdots \, 9$ nên $ 2457 \, \vdots \, 9.$
+) Số $360$ có tổng các chữ số là $3+6+0=9 \, \vdots \, 9$ nên $ 360 \, \vdots \, 9.$
Các số còn lại $354; 1617; 152$ đều có tổng các chữ số không chia hết cho $9$ nên chúng không chia hết cho $9$.
Số liền trước số \(1000\) là
-
A.
\(1002\)
-
B.
\(990\)
-
C.
\(1001\)
-
D.
\(999\)
Đáp án : D
+ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị
+ Số tự nhiên liền trước số \(a\) là số $a - 1.$
Số tự nhiên liền trước số \(1000\) là số \(1000 - 1 = 999.\)
Chọn khẳng định đúng:
-
A.
Mọi số tự nhiên đều có ước chung với nhau.
-
B.
Mọi số tự nhiên đều có ước là $0$ .
-
C.
Số nguyên tố chỉ có đúng $1$ ước là chính nó.
-
D.
Hai số nguyên tố khác nhau thì không có ước chung.
Đáp án : A
- Áp dụng kiến thức:
Mọi số tự nhiên đều có ước là $1$.
Số nguyên tố có $2$ ước là $1$ và chính nó.
Mọi số nguyên tố khác nhau đều có ước chung duy nhất là $1$.
A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$.
B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.
C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.
D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.
 Bình nói: “\(a + b = b + a\)”. Đúng hay sai?
Bình nói: “\(a + b = b + a\)”. Đúng hay sai?
Khi đổi chỗ các số hạng trong một tổng thì tổng đó không thay đổi.
Nên : “\(a + b = b + a\) ”.
Vậy Bình nói đúng.
Tập hợp số tự nhiên được kí hiệu là
-
A.
\(N\)
-
B.
\({N^*}\)
-
C.
\(\left\{ N \right\}\)
-
D.
\(Z\)
Đáp án : A
Tập hợp số tự nhiên kí hiệu là N.
Cho \(A = 90.17 + 34.40 + 12.51\) và \(B = 5.7.9 + 2.5.6\) . Chọn câu đúng.
-
A.
A là số nguyên tố, B là hợp số
-
B.
A là hợp số, B là số nguyên tố
-
C.
Cả A và B là số nguyên tố
-
D.
Cả A và B đều là hợp số
Đáp án : D
+ Dựa vào tính chia hết của một tổng để xét xem A, B có chia hết cho số nào khác \(1\) hay không?
+ Sử dụng định nghĩa số nguyên tố và hợp số để xác định xem A, B là số nguyên tố hay hợp số.
+) Ta có \(A = 90.17 + 34.40 + 12.51\)
Nhận thấy \(17 \, \vdots \, 17;\,34 \, \vdots \, 17;51 \, \vdots \, 17\) nên \(A = 90.17 + 34.40 + 12.51\) chia hết cho \(17\) nên ngoài ước là \(1\) và chính nó thì \(A\) còn có ước là \(17\). Do đó \(A\) là hợp số.
+) Ta có \(B = 5.7.9 + 2.5.6 = 5.\left( {7.9 + 2.6} \right) \, \vdots \, 5\) nên \(B = 5.7.9 + 2.5.6\) ngoài ước là \(1\) và chính nó thì \(A\) còn có ước là \(5\). Do đó \(B\) là hợp số.
Vậy cả \(A\) và \(B\) đều là hợp số.
-
A.
Hình con sao biển có trục đối xứng
-
B.
Hình chiếc lá có trục đối xứng
-
C.
Hai hình đều có trục đối xứng.
-
D.
Không có hình nào có trục đối xứng
Đáp án : A

Vậy hình con sao biển có trục đối xứng.
Lớp 6A có 45 học sinh, có thể chia lớp thành hai nhóm, mỗi nhóm có số lượng học sinh bằng nhau.
Mỗi nhóm có số lượng học sinh bằng nhau có nghĩa là tổng số học sinh của lớp phải chia hết cho 2.
Để mỗi nhóm có số lượng học sinh bằng nhau thì 45 phải chia hết cho 2.
Điều này không xảy ra vì chữ số tận cùng của 45 là 5 nên 45 không chia hết cho 2.
-
A.
\(MQ = NR\)
-
B.
\(MH = RQ\)
-
C.
\(MN = HR\)
-
D.
\(MH = MQ\)
Đáp án : D
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Hình lục giác đều MNPQRH có 3 đường chéo chính bằng nhau nên: \(MQ = NR\)
=> A đúng
Hình lục giác đều MNPQRH có 6 cạnh bằng nhau nên \(MH = RQ\) và \(MN = HR\)
=> B, C đúng.
Do MH là cạnh, MQ là đường chéo chính nên hai đoạn này không bằng nhau
=> D sai
Các số có chữ số tận cùng là … thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
-
A.
0, 1, 2, 3
-
B.
0, 2, 4, 6, 8
-
C.
1, 3, 5, 7, 9
-
D.
0 hoặc 5
Đáp án : D
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Chọn câu đúng.
-
A.
\({5^2}{.5^3}{.5^4} = {5^{10}}\)
-
B.
\({5^2}{.5^3}:{5^4} = 5\)
-
C.
\({5^3}:5 = 5\)
-
D.
\({5^1} = 1\)
Đáp án : B
Sử dụng các công thức ${a^m}.{a^n} = {a^{m + n}}$; ${a^m}:{a^n} = {a^{m - n}}$ \(\left( {a \ne 0;\,m \ge n \ge 0} \right)\)
+) Ta có \({5^2}{.5^3}{.5^4} = {5^{2 + 3 + 4}} = {5^9}\) nên A sai.
+) \({5^2}{.5^3}:{5^4} = {5^{2 + 3 - 4}} = {5^1} = 5\) nên B đúng
+) \({5^3}:5 = {5^{3 - 1}} = {5^2};\,{5^1} = 5\) nên C;D sai.
$BCNN(9;24)$ là bao nhiêu?
-
A.
$54$
-
B.
$18$
-
C.
$72$
-
D.
$36$
Đáp án : C
Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.
Bước 2 : Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3 : Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Ta có:
$\begin{array}{l}9 = {3^2};24 = {2^3}.3\\ \Rightarrow BCNN\left( {9;24} \right) = {2^3}{.3^2} = 8.9 = 72\end{array}$
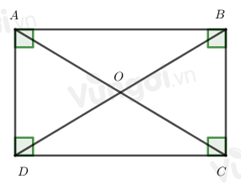
-
A.
\(AB = AC\)
-
B.
\(AC = DO\)
-
C.
\(AC = BD\)
-
D.
\(OB = AC\)
Đáp án : C
Trong hình chữ nhật hai đường chéo bằng nhau
Trong hình chữ nhật hai đường chéo bằng nhau nên \(AC = BD\) => Đáp án C đúng
Đáp án A sai do AB là cạnh, AC là đường chéo nên chúng không bằng nhau.
Đáp án B sai do AC là đường chéo, DO là một nửa đường chéo còn lại nên chúng không bằng nhau.
Đáp án D sai do OB là một nửa đường chéo, AC là đường chéo còn lại nên chúng không bằng nhau.
Tìm số tự nhiên $x$ thỏa mãn: $7+x=362$.
-
A.
300
-
B.
355
-
C.
305
-
D.
362
Đáp án : B
Tìm số hạng chưa biết: Lấy tổng trừ đi số hạng đã biết.
Ta có:
$7+x=362$
$x=362-7$
$x=355$.
Cho các số \(21;77;71;101\). Chọn câu đúng.
-
A.
Số \(21\) là hợp số, các số còn lại là số nguyên tố
-
B.
Có hai số nguyên tố và hai hợp số trong các số trên.
-
C.
Chỉ có một số nguyên tố còn lại là hợp số
-
D.
Không có số nguyên tố nào trong các số trên
Đáp án : B
+ Tìm các ước của các số \(21;77;71;101\)
+ Dùng định nghĩa số nguyên tố và hợp số để tìm các số nguyên tố và hợp số
+ Số \(21\) có các ước \(1;3;7;21\) nên \(21\) là hợp số
+ Số \(77\) có các ước \(1;7;11;77\) nên \(77\) là hợp số
+ Số \(71\) chỉ có hai ước là \(1;71\) nên \(71\) là số nguyên tố.
+ Số \(101\) chỉ có hai ước là \(1;101\) nên \(101\) là số nguyên tố.
Như vậy có hai số nguyên tố là \(71;101\) và hai hợp số là \(21;77.\)
Khẳng định nào sau đây đúng ?
-
A.
B\(\left( 2 \right) = \left\{ {0,2,4,6,8,...} \right\}\)
-
B.
B\(\left( 2 \right) = \left\{ {0;2;4;6;8;...} \right\}\)
-
C.
B \(\left( 2 \right) = \left\{ {2;4;6;8;...} \right\}\)
-
D.
B\(\left( 2 \right) = \left\{ {1;2;4;6;8;...} \right\}\)
Đáp án : B
Ta có thể tìm các bội của một số tự nhiên \(a\) khác \(0\) bằng cách nhân số đó lần lượt với \(0,1,2,3,...\)
Ta lấy 2 nhân với số 0 thì được 0 nên 0 là bội của 2, lấy 2.1=2 nên 2 là bội của 2, 2.2=4 nên 4 là bội của 2,...
Vậy B \(\left( 2 \right) = \left\{ {0;2;4;6;8;...} \right\}\)
Chọn câu đúng:
-
A.
Chu vi của một hình bình hành bằng tổng một cặp cạnh kề nhau bất kỳ.
-
B.
Chu vi hình bình hành bằng tổng của cạnh đáy và chiều cao.
-
C.
Chu vi hình bình hành bằng tích của cạnh đáy nhân với chiều cao.
-
D.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Đáp án : D
Sử dụng công thức tính chu vi hình bình hành.
Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
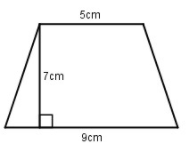
-
A.
\(49\,cm\)
-
B.
\(49\,\,c{m^2}\)
-
C.
\(98\,\,c{m^2}\)
-
D.
\(98\,\,cm\)
Đáp án : B
- Diện tích của hình thang bằng tổng độ dài hai đáy nhân với chiều cao rồi chia đôi.
\(S = \dfrac{{(a + b).h}}{2}\)
Diện tích hình thang đã cho là: \(\frac{{\left( {5 + 9} \right).7}}{2} = 49\,\,\left( {c{m^2}} \right)\)
Sau khi phân tích 45, 150 ra các thừa số nguyên tố được 45 = 3 2 .5 và 150 = 2.3.5 2 . Số mũ nhỏ nhất của thừa số chung 3 là
-
A.
1
-
B.
2
-
C.
3
-
D.
0
Đáp án : A
Xác định số mũ của thừa số 3 trong hai số 45 và 150.
Chọn ra số nhỏ nhất làm số mũ nhỏ nhất.
45 = 3 2 .5 nên số mũ của 3 là 2
150 = 2.3.5 2 nên số mũ của 3 là 1
Số nhỏ nhất là 1 nên số mũ nhỏ nhất của thừa số chung 3 khi phân tích 45 và 150 ra tích các thừa số nguyên tố là 1.
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : B
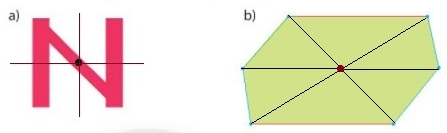
=> Hình a và hình b là hình có tâm đối xứng.
Vậy có 2 hình có tâm đối xứng.
Cho \(B = \left\{ {2;3;4;5} \right\}\). Chọn câu sai.
-
A.
\(2 \in B\)
-
B.
\(5 \in B\)
-
C.
\(1 \notin B\)
-
D.
\(6 \in B\)
Đáp án : D
Áp dụng cách sử dụng kí hiệu \( \in \):
Ví dụ:
+) \(2 \in A\) đọc là \(2\) thuộc A hoặc \(2\) là phần tử của A.
+) \(6 \notin A\) đọc là \(6\) không thuộc A hoặc \(6\) không là phần tử của A.
\(2\) và \(5\) là các phần tử của $B$ nên A, B đúng.
\(1\) không là phần tử của $B$ nên C đúng.
Ta thấy \(6\) không là phần tử của tập hợp \(B\) nên \(6 \notin B.\) Do đó D sai.
Cho tam giác ABC có độ dài cạnh AB bằng 12 cm.Tổng độ dài hai cạnh BC và CA hơn độ dài cạnh AB là 7cm, chu vi tam giác ABC bằng:
-
A.
19 cm
-
B.
31 cm
-
C.
17 cm
-
D.
31 dm
Đáp án : B
- Tìm tổng độ dài hai cạnh BC và CA
- Chu vi tam giác ABC = tổng độ dài hai cạnh BC và CA + độ dài cạnh AB.
- Tổng độ dài hai cạnh BC và CA bằng:
12 + 7 = 19 (cm)
- Chu vi tam giác ABC:
12 + 19 = 31 (cm)
Tổng \(1 + 2 + 3 + 4 + ... + 2018\) bằng
-
A.
\(4074342\)
-
B.
\(2037171\)
-
C.
\(2036162\)
-
D.
\(2035152\)
Đáp án : B
+ Tính số các số tự nhiên liên tiếp từ \(1\) đến \(2018\) bằng công thức (số cuối-số đầu)+1
+ Tổng các số tự nhiên liên tiếp từ \(1\) đến \(2018\) được tính bằng công thức
(số cuối+số đầu). số các số hạng :2
Số các số tự nhiên liên tiếp từ \(1\) đến \(2018\) là \(2018 - 1 + 1 = 2018\) số
Như vậy từ \(1\) đến \(2018\) có số các số hạng là $2018.$
Tổng \(1 + 2 + 3 + 4 + ... + 2018\)\( = \left( {2018 + 1} \right).2018:2 = 2037171.\)
Có bao nhiêu số vừa là bội của $5$ vừa là ước của $50$?
-
A.
$4$ số
-
B.
$5$ số
-
C.
$6$ số
-
D.
$7$ số
Đáp án : A
$\,\left\{ \begin{array}{l}B\left( 5 \right) = {\rm{\{ 5}}{\rm{.k| k}} \in {\rm{N\} }}\\Ư(50) = {\rm{\{ x}} \in {\rm{N}}|50 \, \vdots \, x{\rm{\} }}\end{array} \right.$
Gọi $x$ là số vừa là bội của $5$ vừa là ước của $50$.
\(\left\{ \begin{array}{l}x \in B\left( 5 \right)\\x \in Ư\left( {50} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x \in {\rm{\{ 0;}}\,{\rm{5;10;15;20;25;}}...{\rm{\} }}\\x \in {\rm{\{ 1;2;5;10;25;50\} }}\end{array} \right.\)
\( \Rightarrow \,x\, \in \,{\rm{\{ 5;10;25;50\} }}\)
Tìm số tự nhiên \(\overline {145*} \) chia hết cho cả \(3\) và \(5.\)
-
A.
\(1454\)
-
B.
\(1450\)
-
C.
\(1455\)
-
D.
\(1452\)
Đáp án : C
+ Các số chia hết cho \(5\) có chữ số tận cùng là \(0\) hoặc \(5.\)
+ Các số chia hết cho \(3\) có tổng các chữ số chia hết cho \(3.\)
Từ đó lập luận để tìm các số thỏa mãn.
Vì \(\overline {145*} \) chia hết cho \(5\) nên \(*\) có thể bằng \(0\) hoặc \(5.\)
+ Nếu \(*\) bằng \(0\) thì ta được số \(1450\) có \(1 + 4 + 5 + 0 = 10\not \vdots 3\) nên loại
+ Nếu \(*\) bằng \(5\) thì ta được số \(1455\) có \(1 + 4 + 5 + 5 = 15 \vdots 3\) nên thỏa mãn.
Vậy số cần tìm là \(1455.\)
Nếu cho 7 hình vuông đơn vị ghép thành hình chữ nhật thì có mấy cách xếp (Không kể việc xoay chiều dài và chiều rộng)?
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : A
Hình vuông đơn vị là hình vuông có cạnh bằng 1.
Để xếp các hình vuông đơn vị thành hình chữ nhật thì số lượng hình vuông phải chia hết cho độ dài các cạnh của hình chữ nhật.
Nếu xếp 7 hình vuông đơn vị thành hình chữ nhật thì chiều rộng của hình chữ nhật chỉ có thể xếp:

Tìm tất cả các số tự nhiên \(n\) để \({n^2} + 12n\) là số nguyên tố.
-
A.
$n = 11$
-
B.
$n = 13$
-
C.
$n = 2$
-
D.
$n = 1$
Đáp án : D
+ Phân tích \({n^2} + 12n = n\left( {n + 12} \right)\)
+ Dựa vào định nghĩa số nguyên tố để lập luận và suy ra các giá trị của \(n.\)
Ta có \({n^2} + 12n = n\left( {n + 12} \right);\,n + 12 > 1\) nên để \({n^2} + 12n\) là số nguyên tố thì \(n = 1.\)
Thử lại \({n^2} + 12n = {1^2} + 12.1 = 13\) (nguyên tố)
Vậy với \(n = 1\) thì \({n^2} + 12n\) là số nguyên tố.
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ \(800\) đến \(900\) em.
-
A.
$845$
-
B.
$840$
-
C.
$860$
-
D.
$900$
Đáp án : A
+ Sử dụng kiến thức về phép chia có dư.
+ Sử dụng kiến thức về bội chung và bội chung nhỏ nhất.
+ Sử dụng cách tìm bội chung thông qua bội chung nhỏ nhất.
Gọi số học sinh đi thăm quan là \(x\,\left( {x \in {N^*};\,800 \le x \le 900} \right)\) (học sinh)
Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi nghĩa là thừa ra 5 học sinh nên ta có
\(\left( {x - 5} \right) \vdots 35;\,\left( {x - 5} \right) \vdots 40\) suy ra \(\left( {x - 5} \right) \in BC\left( {35;40} \right)\).
Ta có \(35 = 5.7;\,40 = {2^3}.5\) nên \(BCNN\left( {35;40} \right) = {2^3}.5.7 = 280.\)
Suy ra \((x-5) \in BC\left( {35;40} \right) = B\left( {280} \right) = \left\{ {280;560;840;1120;...} \right\}\) mà \(800 \le x \le 900\) nên \(x -5= 840\) hay $x=845.$
Vậy số học sinh đi thăm quan là \(845\) học sinh.
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều

-
A.
8
-
B.
2
-
C.
4
-
D.
6
Đáp án : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
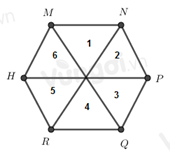
Ta đánh số như hình trên
Nhận thấy có các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.
Tính diện tích của hình thoi có tổng độ dài hai đường chéo là 30cm và đường chéo lớn hơn đường chéo bé 2cm.
-
A.
110 cm 2
-
B.
112 cm 2
-
C.
111 cm 2
-
D.
114 cm 2
Đáp án : B
- Độ dài đường chéo lớn = (Tổng độ dài hai đường chéo + Hiệu độ dài hai đường chéo) : 2
=> Độ dài đường chéo bé = Tổng độ dài hai đường chéo - Độ dài đường chéo lớn
- Diện tích hình thoi bằng nửa tích hai đường chéo: \(S = \frac{{m.n}}{2}\).
Độ dài đường chéo lớn là: \(\left( {30 + 2} \right):2 = 16\,\left( {cm} \right)\)
Độ dài đường chéo bé là: \(30 - 16 = 14\left( {cm} \right)\)
Diện tích hình thoi là: \(\frac{{16.14}}{2} = 112\left( {c{m^2}} \right)\)
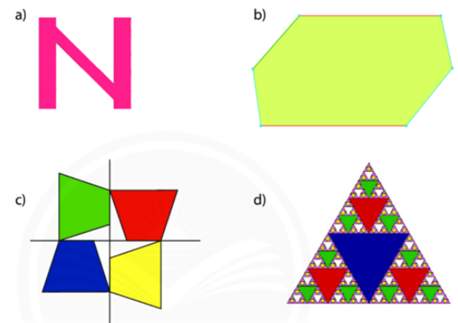
-
A.
Tam giác đều, trái tim, cánh diều
-
B.
Cánh quạt, trái tim, cánh diều
-
C.
Trái tim, Cánh diều
-
D.
Cả bốn hình
Đáp án : D
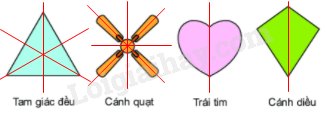
Những hình có trục đối xứng: tam giác đều, cánh quạt, trái tim, cánh diều.
Tìm số tự nhiên n lớn nhất có $3$ chữ số sao cho $n$ chia $8$ dư $7,$ chia $31$ dư $28.$
-
A.
$927$
-
B.
$183$
-
C.
$431$
-
D.
$729$
Đáp án : A
Bước 1: Vì $n$ chia $8$ dư $7,$ chia $31$ dư $28 $ nên: $\left( {n - 7} \right) \vdots 8$ và $\left( {n - 28} \right) \vdots 31$ $\left( {n > 28} \right)$ Bước 2 : Biến đổi tìm số tự nhiên $m$ sao cho $\left( {n + m} \right) \vdots 8$ và $\left( {n + m} \right) \vdots 31$ Khi đó $\left( {n + m} \right) \vdots BCNN\left( {8;31} \right)$ Bước 3: Tìm các giá trị của $n$ Chọn giá trị của $n$ thỏa mãn $n$ là số lớn nhất có $3$ chữ số
Vì $n$ chia $8$ dư $7$ nên $\left( {n - 7} \right) \vdots 8\,\,\,\,\left( {n > 7} \right)$ $ \Rightarrow n = 8a + 7$ với $a \in \mathbb{N}$$ \Rightarrow \left( {n + 1} \right) \vdots 8$
Vì $n$ chia $31$ dư $28$ nên $\left( {n - 28} \right) \vdots 31\left( {n > 28} \right)$ $ \Rightarrow n = 31b + 28$ $\left( {b \in \mathbb{N}} \right)$ $ \Rightarrow \left( {n + 3} \right) \vdots 31$ Vì $64 \vdots 8$ nên $\left( {n + 1 + 64} \right) \vdots 8$ hay $\left( {n + 65} \right) \vdots 8\left( 1 \right)$ Vì $62 \vdots 31$ $ \Rightarrow \left( {n + 3 + 62} \right) \vdots 31$ hay $\left( {n + 65} \right) \vdots 31$ (2) Từ (1) và (2) $ \Rightarrow \left( {n + 65} \right) \vdots $$BCNN\left( {8;31} \right)$ $ \Rightarrow \left( {n + 65} \right) \vdots 248$ $ \Rightarrow n = 248k - 65$ $\left( {k \in {\mathbb{N}^ * }} \right)$ Với $k = 1$ $ \Rightarrow n = 248.1 - 65 = 183$ Với $k = 2 \Rightarrow n = 248.2 - 65 = 431$ Với $k = 3 \Rightarrow n = 248.3 - 65 = 679$ Với $k = 4 \Rightarrow n = 248.4 - 65 = 927$ Với $k = 5 \Rightarrow n = 248.5 - 65 = 1175$ (loại) Vì $n$ là số lớn nhất có $3$ chữ số nên $n = 927.$
Cho \(P = 1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}\). Chọn đáp án đúng.
-
A.
\(123.P = {5^{102}} - 1\)
-
B.
\(124.P = {5^{102}} - 1\)
-
C.
\(124.P = {5^{101}} - 1\)
-
D.
\(124.P = {5^{102}}\)
Đáp án : B
Nhân thêm vào hai vế của biểu thức $P$ với \({5^3}\) để được biểu thức mới, sau đó lấy biểu thức mới trừ đi biểu thức ban đầu, biến đổi để được biểu thức rút gọn của $P$.
\(\begin{array}{l}P = 1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}\\{5^3}.P = {5^3}.\left( {1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}} \right) = {5^3} + {5^6} + {5^9} + ... + {5^{99}} + {5^{102}}\\125.P = {5^3} + {5^6} + {5^9} + ... + {5^{99}} + {5^{102}}\\ \Rightarrow 125.P - P = \left( {{5^3} + {5^6} + {5^9} + ... + {5^{99}} + {5^{102}}} \right) - \left( {1 + {5^3} + {5^6} + {5^9} + ... + {5^{99}}} \right)\\ \Rightarrow 124.P = {5^{102}} - 1\end{array}\)
Sân trường em hình vuông. Để tăng thêm diện tích nhà trường mở rộng về mỗi phía 4m thì diện tích tăng thêm 192m 2 . Hỏi trước đây sân trường em có diện tích là bao nhiêu m 2 ?
-
A.
16 m 2
-
B.
32 m 2
-
C.
64 m 2
-
D.
128 m 2
Đáp án : C
- Diện tích tăng thêm bằng diện tích 4 hình vuông nhỏ cạnh bằng 4m và 4 hình chữ nhật có 1 cạnh bằng 4 m và 1 cạnh bằng cạnh hình vuông
- Tinh diện tích 4 hình vuông nhỏ
- Tính diện tích 4 hình chữ nhật
- Tính diện tích 1 hình chữ nhật
- Tính cạnh hình vuông đã cho
=> Diện tích sân trường lúc chưa mở rộng.
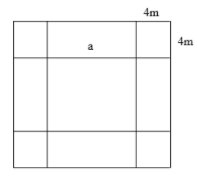
Diện tích tăng thêm bằng diện tích 4 hình vuông nhỏ cạnh bằng 4m và 4 hình chữ nhật có 1 cạnh bằng 4 m và 1 cạnh bằng cạnh hình vuông
Diện tích 4 hình vuông nhỏ là: 4 . (4 . 4) = 64 m 2
Diện tích 4 hình chữ nhật là: 192 - 64 = 128 m 2
Diện tích 1 hình chữ nhật là 128 : 4 = 32 m 2
Cạnh hình vuông đã cho là: 32 : 4 = 8 m
Diện tích sân trường lúc chưa mở rộng là: 8 . 8 = 64 m 2
Toán vui. Hai bạn Na và Toàn đứng đối diện nhau trên nền đất, ở giữa họ có một dãy các số và dấu cộng như hình dưới đây. Do vị trí nhìn khác nhau nên hai bạn thấy hai dãy các phép tính khác nhau.

Phép tính Toàn quan sát được để phép tính hai bạn quan sát thấy bằng nhau là:
-
A.
\({\bf{11}} + {\bf{8}}1 + 1{\bf{9}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{270}} \)
-
B.
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{275}} \)
-
C.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
-
D.
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{6}}8 + {\bf{9}}1 + 11{\rm{ }} = {\bf{344}} \)
Đáp án : C
Điền các số: 1; 6; 8; 9 vào ô trống để được phép tính đúng.
Phép tính Toàn quan sát được là:
\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)
Phép tính Na quan sát được là:
\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{69}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{344}} \)