Giải bài 1. 45 trang 32 sách bài tập toán 12 - Kết nối tri thức — Không quảng cáo

Đề bài

Chứng tỏ rẳng một thùng hình trụ có thể tích $V$ cố định cần ít vật liệu sản xuất nhất (tức là có diện tích bề mặt nhỏ nhất) khi chiều cao của thùng gấp đôi bán kính đáy.

Lời giải chi tiết

Gọi bán kính đáy của thùng hình trụ là $r$, $r > 0$. Khi đó diện tích một đáy hình trụ là $\pi {r^2}$.

Suy ra chiều cao của hình trụ là $\frac{V}{{\pi {r^2}}}$.

Do đó diện tích bề mặt hình trụ là $S = 2\pi {r^2} + 2\pi r\frac{V}{{\pi {r^2}}} = 2\pi {r^2} + \frac{{2V}}{r}$

Xét hàm số  $S = 2\pi {r^2} + \frac{{2V}}{r},r > 0$. Ta cần tìm giá trị nhỏ nhất của hàm $S$ trên $\left( {0; + \infty } \right)$.

Ta có $S' = 4\pi r - \frac{{2V}}{{{r^2}}} = \frac{{4\pi {r^3} - 2V}}{{{r^2}}}$ khi đó $S' = 0 \Leftrightarrow \frac{{4\pi {r^3} - 2V}}{{{r^2}}} = 0 \Leftrightarrow r = \sqrt[3]{{\frac{V}{{2\pi }}}}$.

Lập bảng biến thiên

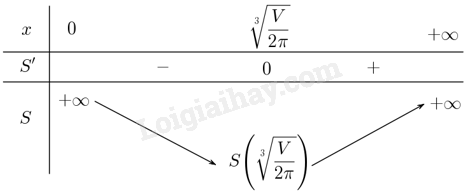
Từ bảng biến thiên suy ra $S$ đạt giá trị lớn nhất khi $r = \sqrt[3]{{\frac{V}{{2\pi }}}}$, ta thấy chiều cao hình trụ khi đó là $\frac{V}{{\pi {r^2}}} = \frac{V}{{\pi {{\left( {\sqrt[3]{{\frac{V}{{2\pi }}}}} \right)}^2}}} = \frac{V}{{\left( {\pi  \cdot \frac{{{V^{\frac{2}{3}}}}}{{{{\left( {2\pi } \right)}^{\frac{2}{3}}}}}} \right)}} = \frac{V}{{\frac{{\sqrt[3]{\pi }}}{{\sqrt[3]{4}}} \cdot {V^{\frac{2}{3}}}}} = \frac{{\sqrt[3]{V} \cdot \sqrt[3]{4}}}{{\sqrt[3]{\pi }}} = \frac{{2\sqrt[3]{V}}}{{\sqrt[3]{{2\pi }}}} = 2r$.

Vậy để vật liệu sản xuất thùng ít nhất thì chiều cao gấp đôi bán kính đáy (điều phải chứng minh).