Giải bài 1.48 trang 32 sách bài tập toán 12 - Kết nối tri thức
Một công ty ước tính rằng chi phí (C) (USD) để sản xuất (x) đơn vị sản phẩm có thể được mô hình hóa bằng công thức (C = 800 + 0,04x + 0,0002{x^2}). Tìm mức sản xuất sao cho chi phí trung bình (overline C left( x right) = frac{{Cleft( x right)}}{x}) cho mỗi đơn vị hàng hóa là nhỏ nhất.
Đề bài
Một công ty ước tính rằng chi phí \(C\) (USD) để sản xuất \(x\) đơn vị sản phẩm có thể được mô hình hóa bằng công thức
\(C = 800 + 0,04x + 0,0002{x^2}\).
Tìm mức sản xuất sao cho chi phí trung bình \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\) cho mỗi đơn vị hàng hóa là nhỏ nhất.
Phương pháp giải - Xem chi tiết
+ Viết công thức \(\overline C \left( x \right)\).
+ Tìm \(x > 0\) để \(\overline C \left( x \right)\) nhỏ nhất.
Lời giải chi tiết
Ta có \(\overline C \left( x \right) = \frac{{800 + 0,04x + 0,0002{x^2}}}{x} = \frac{{800}}{x} + 0,04 + 0,0002x\), \(x > 0\)
Chi phí trung bình nhỏ nhất khi \(\overline C \left( x \right)\) đạt giá trị nhỏ nhất, ta cần tìm \(x\) để \(\overline C \left( x \right)\) nhỏ nhất.
Ta có \(\overline {C'} \left( x \right) = \frac{{ - 800}}{{{x^2}}} + 0,0002 = \frac{{ - 800 + 0,0002{x^2}}}{{{x^2}}}\).
Khi đó \(\overline {C'} \left( x \right) = 0 \Leftrightarrow \frac{{ - 800 + 0,0002{x^2}}}{{{x^2}}} = 0 \Leftrightarrow - 800 + 0,0002{x^2} = 0 \Leftrightarrow x = 2000\) vì \(x > 0\).
Lập bảng biến thiên
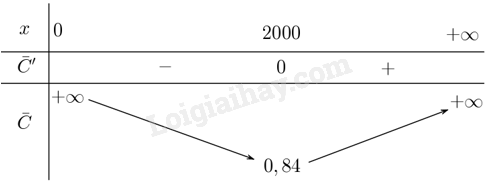
Từ bảng biến thiên suy ra \(\overline C \left( x \right)\) đạt giá trị nhỏ nhất khi \(x = 2000\).
Vậy với mức sản xuất \(2000\) thì chi phí trung bình cho mỗi đơn vị hàng hóa là nhỏ nhất.