Giải bài 1.63 trang 36 sách bài tập toán 12 - Kết nối tri thức
Cho hàm số (y = frac{1}{3}{x^3} + left( {m - 1} right){x^2} + left( {2m - 3} right)x + frac{2}{3}). a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi (m = 2). b) Tìm (m) để hàm số có hai điểm cực trị ({x_1}) và ({x_2}) thỏa mãn (x_1^2 + x_2^2 = 5). c) Tìm (m) để hàm số đồng biến trên (mathbb{R}). d) Tìm (m) để hàm số đồng biến trên khoảng (left( {1; + infty } right)).
Đề bài
Cho hàm số \(y = \frac{1}{3}{x^3} + \left( {m - 1} \right){x^2} + \left( {2m - 3} \right)x + \frac{2}{3}\).
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi \(m = 2\).
b) Tìm \(m\) để hàm số có hai điểm cực trị \({x_1}\) và \({x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 5\).
c) Tìm \(m\) để hàm số đồng biến trên \(\mathbb{R}\).
d) Tìm \(m\) để hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
Phương pháp giải - Xem chi tiết
Ý a: Thay \(m = 2\) và hàm số sau đó khảo sát sự biến thiên và vẽ đồ thị hàm số,
Ý b: Xét phương trình hoành độ giao điểm của hai đồ thị, tìm điều kiện để phương trình đó có hai nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 5\), sử dụng định lý Viète mà một số biến đổi cơ bản để giải ra m.
Ý c: Hàm số đồng biến trên \(\mathbb{R}\) khi \(y' \ge 0\forall x \in \mathbb{R}\). Sử dụng kiến thức về dấu, nghiệm của tam thức bậc hai để làm.
Ý d: Kết hợp với bảng biến thiên để giải bài toán, lưu ý xét hết các trường hợp.
Lời giải chi tiết
a) Khi \(m = 2\) hàm số trở thành \(y = \frac{1}{3}{x^3} + {x^2} + x + \frac{2}{3}\).
Tập xác định: \(\mathbb{R}\).
+ Sự biến thiên:
Ta có \(y' = {x^2} + 2x + 1 = {\left( {x + 1} \right)^2} \ge 0\) với mọi \(x \in \mathbb{R}\).
Suy ra hàm số đồng biến trên \(\mathbb{R}\) và không có cực trị.
Lập bảng biến thiên:
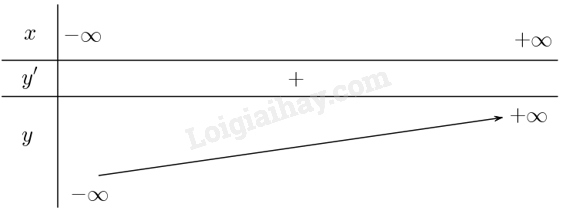
+ Đồ thị: Đồ thị nhận \(\left( { - 1;\frac{1}{3}} \right)\) làm tâm đối xứng.
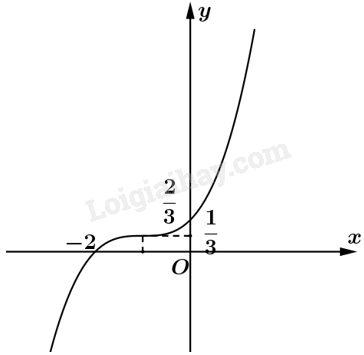
b) Ta có \(y' = {x^2} + 2\left( {m - 1} \right)x + 2m - 3\).
Khi đó \(y' = 0 \Leftrightarrow {x^2} + 2\left( {m - 1} \right)x + 2m - 3 = 0 \Leftrightarrow x = - 1\) hoặc \(x = 3 - 2m\).
Để hàm số có hai cực trị thì đạo hàm \(y'\) phải có hai nghiệm phân biệt \({x_1};{x_2}\), tức là \(3 - 2m \ne - 1 \Leftrightarrow m \ne 2\)
Để \(x_1^2 + x_2^2 = 5\) thì \({\left( {3 - 2m} \right)^2} + 1 = 5 \Leftrightarrow m \in \left\{ {\frac{1}{2};\frac{5}{2}} \right\}\).
c) Hàm số đồng biến trên \(\mathbb{R}\) khi \(y' \ge 0\forall x \in \mathbb{R}\).
Ta có \({x^2} + 2\left( {m - 1} \right)x + 2m - 3 \ge 0 \Leftrightarrow \left\{ \begin{array}{l}1 > 0\\\Delta ' \le 0\end{array} \right. \Leftrightarrow 3 - 2m = - 1 \Leftrightarrow m = 2\).
d) Ta có \(y' = 0 \Leftrightarrow x = - 1\) hoặc \(x = 3 - 2m\).
Trường hợp 1: \( - 1 \le 3 - 2m \Leftrightarrow m \le 2\). Khi đó ta có bảng biến thiên:
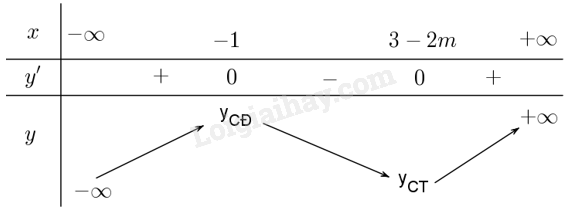
Để hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\) thì \(3 - 2m \le 1 \Leftrightarrow m \ge 1\). Suy ra \(1 \le m < 2\)
Trường hợp 2: \(3 - 2m < - 1 \Leftrightarrow m > 2\). Khi đó ta có bảng biến thiên:
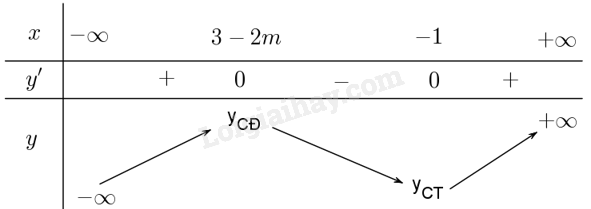
Ta thấy hàm số luôn đồng biến trên \(\left( {1; + \infty } \right)\) nên trường hợp này ta có \(m > 2\).
Vậy \(m \ge 1\).