Giải bài 1 trang 60 sách bài tập toán 12 - Cánh diều
Cho tứ diện (ABCD). Lấy (G) là trọng tâm tam giác (BCD). Phát biểu nào sau đây là sai? A. (overrightarrow {GB} + overrightarrow {GC} + overrightarrow {GD} = overrightarrow 0 ). B. (overrightarrow {GA} + overrightarrow {GB} + overrightarrow {GC} + overrightarrow {GD} = overrightarrow 0 ). C. (overrightarrow {CB} + overrightarrow {CD} = 3overrightarrow {CG} ). D. (overrightarrow {AB} + overrightarrow {AC} + overrightarrow {AD} = 3overrightarrow {AG} ).
Đề bài
Cho tứ diện \(ABCD\). Lấy \(G\) là trọng tâm tam giác \(BCD\). Phát biểu nào sau đây là sai ?
A. \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
C. \(\overrightarrow {CB} + \overrightarrow {CD} = 3\overrightarrow {CG} \)
D. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
Phương pháp giải - Xem chi tiết
‒ Sử dụng tính chất trung điểm của đoạn thẳng và tính chất trọng tâm của tam giác.
Lời giải chi tiết
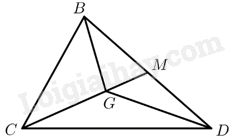
Theo tính chất trọng tâm của tam giác, với \(G\) là trọng tâm tam giác \(BCD\), ta có: \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Vậy A đúng.
Gọi \(M\) là trung điểm của \(BD\). Ta có:
\(\overrightarrow {CB} + \overrightarrow {CD} = 2\overrightarrow {CM} = 2.\frac{2}{3}\overrightarrow {CG} = 3\overrightarrow {CG} \). Vậy C đúng.
Ta có: \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {AG} + \overrightarrow {GB} + \overrightarrow {AG} + \overrightarrow {GC} + \overrightarrow {AG} + \overrightarrow {GD} = 3\overrightarrow {AG} + \left( {\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = 3\overrightarrow {AG} \). Vậy D đúng.
Chọn B.