Giải bài 10 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo
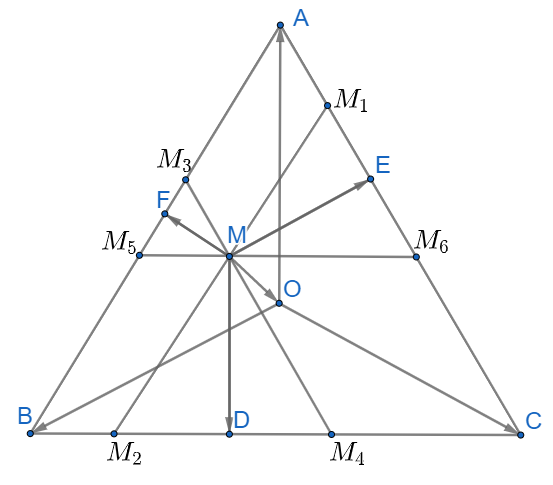
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB.
Đề bài
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)
Phương pháp giải - Xem chi tiết
Bước 1: Qua M kẻ các đường thẳng song song với AB, AC, BC
Bước 2: Xác định các tam giác đều, hình bình hành sau đó áp dụng vào biểu thức vectơ, trong tam giác đều thì đường cao vừa là trung tuyến, quy tắc hình bình hành \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (với ABCD là hình bình hành)
Bước 3: Sử dụng quy tắc ba điểm \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} \), tính chất trọng tâm của tam giác \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) (với G là trọng tâm của tam giác ABC )
Lời giải chi tiết
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \left( {\overrightarrow {MO} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OE} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OF} } \right)\)
Qua M kẻ các đường thẳng \({M_1}{M_2}//AB;{M_3}{M_4}//AC;{M_5}{M_6}//BC\)
Từ đó ta có: \(\widehat {M{M_1}{M_6}} = \widehat {M{M_6}{M_1}} = \widehat {M{M_4}{M_2}} = \widehat {M{M_2}{M_4}} = \widehat {M{M_3}{M_5}} = \widehat {M{M_5}{M_3}} = 60^\circ \)
Suy ra các tam giác \(\Delta M{M_3}{M_5},\Delta M{M_1}{M_6},\Delta M{M_2}{M_4}\) đều
Áp dụng tính chất trung tuyến \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)(với M là trung điểm của BC) ta có:
\(\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right);\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right);\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( \Rightarrow \overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
Ta có: các tứ giác \(A{M_3}M{M_1};C{M_4}M{M_6};B{M_2}M{M_5}\) là hình bình hành
Áp dụng quy tắc hình bình hành ta có
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_3}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_5}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_4}} + \overrightarrow {M{M_6}} } \right)\)
\( = \frac{1}{2}\overrightarrow {MA} + \frac{1}{2}\overrightarrow {MB} + \frac{1}{2}\overrightarrow {MC} = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\)
\( = \frac{1}{2}\left( {\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)} \right)\)
\( = \frac{1}{2}\left( {3\overrightarrow {MO} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)} \right) = \frac{3}{2}\overrightarrow {MO} \) (đpcm)
Vậy \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)