Giải bài 110 trang 44 sách bài tập toán 12 - Cánh diều — Không quảng cáo

Đề bài

Một nhà in sử dụng các trang giấy hình chữ nhật để in sách. Sau khi để lề trái, lề phải, lề trên và lề dưới theo số liệu được cho ở Hình 33 thì diện tích phần in chữ trên trang sách là 24 inch ² . Tính kích thước của trang sách để diện tích giấy cần sử dụng là ít nhất?

Lời giải chi tiết

Chiều dài của trang giấy là: \(x + 1\frac{1}{2} + 1\frac{1}{2} = x + 3\left( {inch} \right)\).

Chiều rộng của trang giấy là: \(y + 1 + 1 = y + 2\left( {inch} \right)\).

Diện tích một trang giấy là: \(S = \left( {x + 3} \right)\left( {y + 2} \right)\left( {inch} \right)\).

Diện tích phần in chữ là: \(xy = 24\). Suy ra \(y = \frac{{24}}{x}\).

Khi đó, \(S = \left( {x + 3} \right)\left( {\frac{{24}}{x} + 2} \right) = 30 + 2{\rm{x}} + \frac{{72}}{x}\)

Xét hàm số \(S\left( x \right) = 30 + 2{\rm{x}} + \frac{{72}}{x}\) trên \(\left( {0; + \infty } \right)\).

Ta có: \(S'\left( x \right) = 2 - \frac{{72}}{{{x^2}}}\)

Khi đó, trên khoảng \(\left( {0; + \infty } \right)\), \(y' = 0\) khi \(x = 6\).

Bảng biến thiên:

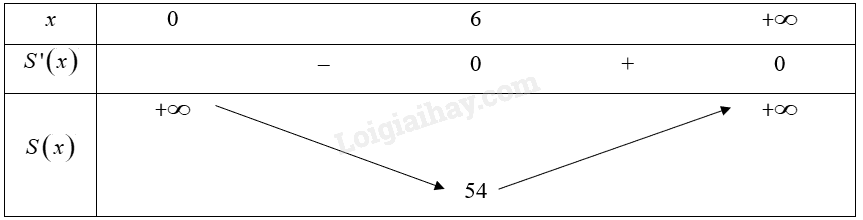
Vậy \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} S\left( x \right) = 54\) tại \(x = 6 \Leftrightarrow y = \frac{{24}}{6} = 4\).

Vậy \(S\) nhỏ nhất khi \(x = 6,y = 4\). Vậy, kích thước của trang sách là \(9\left( {inch} \right) \times 6\left( {inch} \right)\).