Giải bài 17 trang 98 sách bài tập toán 12 - Cánh diều — Không quảng cáo

Đề bài

Bảng 22 thống kê độ ẩm không khí trung bình các tháng năm 2022 tại Đà Nẵng và Quy Nhơn (đơn vị: %).

a) Hãy lần lượt ghép các số liệu của Đà Nẵng, Quy Nhơn thành năm nhóm sau: $\left[ {71;74} \right),$$\left[ {74;77} \right),\left[ {77;80} \right),\left[ {80;83} \right),\left[ {83;86} \right)$.

b) Tính khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm của Đà Nẵng và Quy Nhơn.

Lời giải chi tiết

a) Ta có bảng sau:

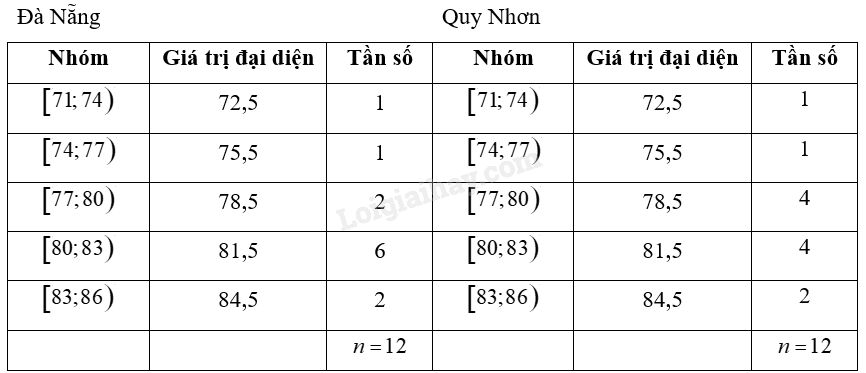
b) • Đà Nẵng:

Khoảng biến thiên của mẫu số liệu ghép nhóm là: $R = 86 - 71 = 15$.

Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\frac{n}{4} = \frac{{12}}{4} = 3$.

Nhóm 3 có đầu mút trái $s = 77$, độ dài $h = 3$, tần số của nhóm ${n_3} = 2$ và nhóm 2 có tần số tích luỹ $c{f_2} = 1 + 1 = 2$.

Ta có: ${Q_1} = s + \left( {\frac{{3 - c{f_2}}}{{{n_3}}}} \right).h = 77 + \left( {\frac{{3 - 2}}{2}} \right).3 = 78,5$ (%).

Nhóm 4 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\frac{{3n}}{4} = \frac{{3.12}}{4} = 9$.

Nhóm 4 có đầu mút trái $t = 80$, độ dài $l = 3$, tần số của nhóm ${n_4} = 6$ và nhóm 3 có tần số tích luỹ $c{f_3} = 1 + 1 + 2 = 4$.

Ta có: ${Q_3} = t + \left( {\frac{{9 - c{f_3}}}{{{n_4}}}} \right).l = 80 + \left( {\frac{{9 - 4}}{6}} \right).3 = 82,5$ (%).

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: $\Delta Q = {Q_3} - {Q_1} = 82,5 - 78,5 = 4$ (%).

Số trung bình cộng của mẫu số liệu ghép nhóm là:

$\overline x  = \frac{{1.72,5 + 1.75,5 + 2.78,5 + 6.81,5 + 2.84,5}}{{12}} = 80,25$

Phương sai của mẫu số liệu ghép nhóm đó là:

$\begin{array}{l}{s^2} = \frac{1}{{12}}\left[ {1.{{\left( {72,5 - 80,25} \right)}^2} + 1.{{\left( {75,5 - 80,25} \right)}^2} + 2.{{\left( {78,5 - 80,25} \right)}^2} + 6.{{\left( {81,5 - 80,25} \right)}^2} + } \right.\\\left. { + 2.{{\left( {84,5 - 80,25} \right)}^2}} \right] = 11,1875\end{array}$

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $s = \sqrt {11,1875}  \approx 3,3448$.

• Quy Nhơn:

Khoảng biến thiên của mẫu số liệu ghép nhóm là: $R = 86 - 71 = 15$.

Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\frac{n}{4} = \frac{{12}}{4} = 3$.

Nhóm 3 có đầu mút trái $s = 77$, độ dài $h = 3$, tần số của nhóm ${n_3} = 4$ và nhóm 2 có tần số tích luỹ $c{f_2} = 1 + 1 = 2$.

Ta có: ${Q_1} = s + \left( {\frac{{3 - c{f_2}}}{{{n_3}}}} \right).h = 77 + \left( {\frac{{3 - 2}}{4}} \right).3 = 77,75$ (%).

Nhóm 4 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\frac{{3n}}{4} = \frac{{3.12}}{4} = 9$.

Nhóm 4 có đầu mút trái $t = 80$, độ dài $l = 3$, tần số của nhóm ${n_4} = 4$ và nhóm 3 có tần số tích luỹ $c{f_3} = 1 + 1 + 4 = 6$.

Ta có: ${Q_3} = t + \left( {\frac{{9 - c{f_3}}}{{{n_4}}}} \right).l = 80 + \left( {\frac{{9 - 6}}{4}} \right).3 = 82,25$ (%).

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: $\Delta Q = {Q_3} - {Q_1} = 82,25 - 77,75 = 4,5$ (%).

Số trung bình cộng của mẫu số liệu ghép nhóm là:

$\overline x  = \frac{{1.72,5 + 1.75,5 + 4.78,5 + 4.81,5 + 2.84,5}}{{12}} = 79,75$

Phương sai của mẫu số liệu ghép nhóm đó là:

$\begin{array}{l}{s^2} = \frac{1}{{12}}\left[ {1.{{\left( {72,5 - 79,75} \right)}^2} + 1.{{\left( {75,5 - 79,75} \right)}^2} + 4.{{\left( {78,5 - 79,75} \right)}^2} + 4.{{\left( {81,5 - 79,75} \right)}^2} + } \right.\\\left. { + 2.{{\left( {84,5 - 79,75} \right)}^2}} \right] = 11,1875\end{array}$

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $s = \sqrt {11,1875}  \approx 3,3448$.