Giải bài 17 trang 13 sách bài tập toán 12 - Cánh diều
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số (y = {x^3} - 3{rm{x}} + 2). a) (y' = 3{{rm{x}}^2} - 3). b) (y' = 0) khi (x = - 1,x = 1). c) (y' > 0) khi (x in left( { - 1;1} right)) và (y' < 0) khi (x in left( { - infty ; - 1} right) cup left( {1; + infty } right)). d) Giá trị cực đại của hàm số là ${{f}_{CĐ}}=0$.
Đề bài
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).
Cho hàm số \(y = {x^3} - 3{\rm{x}} + 2\). a) \(y' = 3{{\rm{x}}^2} - 3\). b) \(y' = 0\) khi \(x = - 1,x = 1\). c) \(y' > 0\) khi \(x \in \left( { - 1;1} \right)\) và \(y' < 0\) khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\). d) Giá trị cực đại của hàm số là ${{f}_{C}}=0$.
Phương pháp giải - Xem chi tiết
Lập bảng biến thiên của hàm số \(y = f\left( x \right)\), từ đó xác định các khoảng đơn điệu, cực trị của hàm số \(y = f\left( x \right)\).
Lời giải chi tiết
Hàm số có tập xác định là \(\mathbb{R}\).
Ta có:
\(y' = 3{{\rm{x}}^2} - 3\). Vậy a) đúng.
\(y' = 0\) khi \(x = - 1,x = 1\). Vậy b) đúng.
Bảng biến thiên của hàm số:
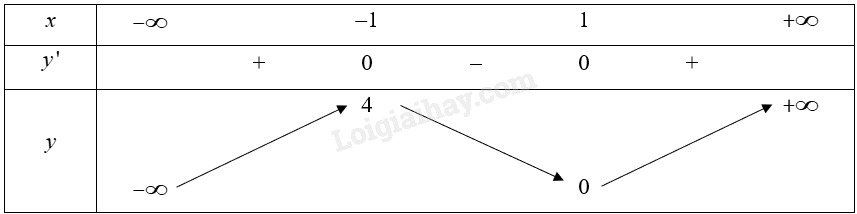
Vậy hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\); nghịch biến trên khoảng \(\left( { - 1;1} \right)\). Vậy c) sai.
Hàm số đạt cực đại tại \(x = - 1\). Khi đó giá trị cực đại ${{f}_{CĐ}}=4$. Vậy d) sai.
a) Đ. b) Đ. c) S. d) S.