Giải bài 16 trang 95 sách bài tập toán 12 - Cánh diều
Một đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xác suất bắn trúng mục tiêu của xạ thủ hạng I và hạng II lần lượt là 0,75 và 0,6. Chọn ngẫu nhiên một xạ thủ và xạ thủ đó chỉ bắn 1 viên đạn. Sử dụng sơ đồ hình cây, tính xác suất để viên đạn đó trúng mục tiêu.
Đề bài
Một đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xác suất bắn trúng mục tiêu của xạ thủ hạng I và hạng II lần lượt là 0,75 và 0,6. Chọn ngẫu nhiên một xạ thủ và xạ thủ đó chỉ bắn 1 viên đạn. Sử dụng sơ đồ hình cây, tính xác suất để viên đạn đó trúng mục tiêu.
Phương pháp giải - Xem chi tiết
‒ Sử dụng sơ đồ hình cây.
‒ Sử dụng công thức tính xác suất toàn phần: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Lời giải chi tiết
Xét các biến cố:
\(A\): “Chọn được xạ thủ hạng I”;
\(B\): “Viên đạn đó trúng mục tiêu”;
Có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II nên ta có
\(P\left( A \right) = \frac{4}{{10}} = 0,4;P\left( {\overline A } \right) = \frac{6}{{10}} = 0,6\)
Xác suất bắn trúng mục tiêu của xạ thủ hạng I và 0,75 nên ta có \(P\left( {B|A} \right) = 0,75\).
Xác suất bắn trúng mục tiêu của xạ thủ hạng II và 0,6 nên ta có \(P\left( {B|\overline A } \right) = 0,6\).
Ta có sơ đồ hình cây như sau:
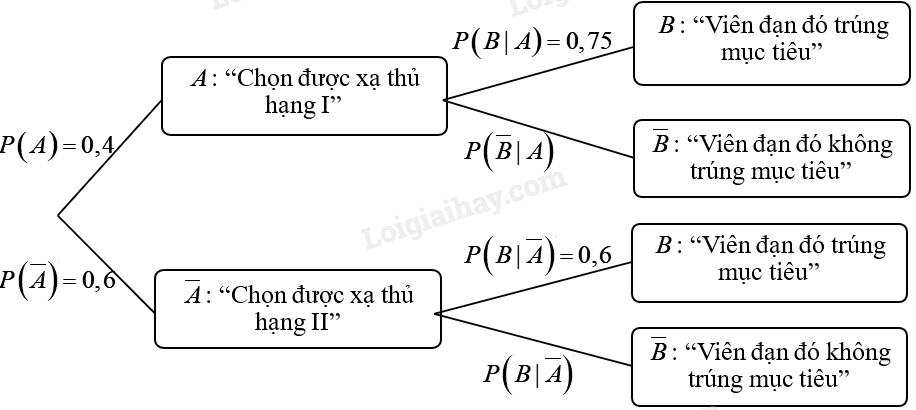
Vậy xác suất của biến cố \(B\): “Viên đạn đó trúng mục tiêu” là:
\(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right) = 0,4.0,75 + 0,6.0,6 = 0,66\).