Giải bài 19 trang 74 sách bài tập toán 8 - Chân trời sáng tạo
Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc (widehat {ADB},widehat {DBC}left( {E in AB,K in CD} right))
Đề bài
Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc \(\widehat {ADB},\widehat {DBC}\left( {E \in AB,K \in CD} \right)\)
a) Chứng minh DE//BK.
b) Giả sử \(DE \bot AB\). Chứng minh \(DA = DB\).
c) Trong trường hợp \(DE \bot AB\), tìm số đo của \(\widehat {ADB}\) để tứ giác DEBK là hình vuông.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có hai cạnh đối song song.
b) Sử dụng kiến thức về dấu hiệu nhận biết tam giác cân để chứng minh: Tam giác có đường cao đồng thời là đường phân giác thì tam giác đó là tam giác cân.
c) Sử dụng dấu hiệu nhận biết hình vuông để chứng minh: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
Lời giải chi tiết
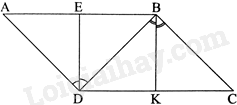
a) Vì ABCD là hình bình hành nên AD//BC. Suy ra \(\widehat {ADB} = \widehat {DBC}\) (hai góc so le trong)
Do đó: \(\frac{{\widehat {ADB}}}{2} = \frac{{\widehat {DBC}}}{2}\), suy ra \(\widehat {EDB} = \widehat {KBD}\)
Mà hai góc này ở vị trí so le trong nên DE//BK.
b) Tam giác DAB có DE vừa là đường cao đồng thời là phân giác nên tam giác DAB cân tại D. Do đó, \(DA = DB\)
c) Tứ giác DEBK có: DE//BK, EB//DK nên tứ giác DEBK là hình bình hành. Mà \(\widehat {DEB} = {90^0}\) nên DEBK là hình chữ nhật.
Để hình chữ nhật DEBK là hình vuông thì \(DE = EB\)
Mà tam giác DAB cân tại D nên DE là trung tuyến của tam giác DAB.
Suy ra: \(DE = EB = AE = \frac{{AB}}{2}\), do đó tam giác DAB vuông tại D hay \(\widehat {ADB} = {90^0}\)