Giải bài 20 trang 109 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn (O) và dây AB khác đường kính. Kẻ bán kính OC đi qua trung điểm I của đoạn thẳng AB. Vẽ đường tròn (C; CI). Kẻ tiếp tuyến BD của đường tròn (C) với D là tiếp điểm và D khác I. Chứng minh: a) Bốn đỉnh của tứ giác BDCI cùng nằm trên một đường tròn. b) BD là tiếp tuyến của đường tròn (O).
Đề bài
Cho đường tròn (O) và dây AB khác đường kính. Kẻ bán kính OC đi qua trung điểm I
của đoạn thẳng AB. Vẽ đường tròn (C; CI). Kẻ tiếp tuyến BD của đường tròn (C) với D là tiếp điểm và D khác I. Chứng minh:
a) Bốn đỉnh của tứ giác BDCI cùng nằm trên một đường tròn.
b) BD là tiếp tuyến của đường tròn (O).
Phương pháp giải - Xem chi tiết
a) Gọi M là trung điểm của BC.
Áp dụng: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng 1 nửa cạnh huyền (tam giác IBC và DBC) để suy ra \(MB = MC = MD = MI\).
b) Bước 1: Chứng minh \(\widehat {DCB} = \widehat {OBC}\left( { = \widehat {OCB}} \right)\).
Bước 2: \(\widehat {DCB} + \widehat {CBD} = \widehat {CBO} + \widehat {CBD} = \widehat {OBD} = 90^\circ \).
Lời giải chi tiết
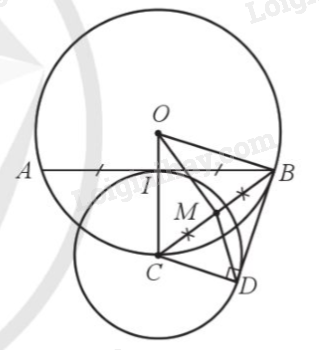
a) Xét tam giác OAB có: \(OA = OB\) (đều bằng bán kính (O)) nên tam giác OAB cân tại O, mà I là trung điểm của AB nên OI là đường trung tuyến đồng thời là đường cao của tam giác OAB, do đó \(OI \bot AB\).
Lấy M là trung điểm của CB nên DM, IM lần lượt là đường trung tuyến của 2 tam giác vuông IBC và DCB, nên ta có \(MB = MC = MD = MI = \frac{{BC}}{2}\).
Do đó 4 đỉnh của tứ giác BDCI cung nằm trên một đường tròn đường kính BC.
b) Để giải phương trình trên, ta giải 2 phương trình sau:
Xét tam giác OBC có \(OB = OC\)(cùng bằng bán kính (O)) nên \(\widehat {OCB} = \widehat {OBC}\) (1)
Xét (C; CI) có AB vuông góc với CI tại I nên AB là tiếp tuyến của (C; CI).
Mặt khác BD cũng là tiếp tuyến của (C;CI).
Suy ra \(\widehat {ICB} = \widehat {DCB}\) (2).
Từ (1) và (2) nên \(\widehat {DCB} = \widehat {OBC}\).
Ta lại có \(\widehat {DCB} + \widehat {DBC} = 90^\circ \) (do tam giác CBD vuông tại D) hay \(\widehat {OBC} + \widehat {DBC} = 90^\circ \), do đó \(\widehat {OBD} = 90^\circ \).
Suy ra \(BD \bot OB\) tại B.
Vậy BD là tiếp tuyến (O).