Giải bài 25 trang 52 sách bài tập toán 12 - Kết nối tri thức — Không quảng cáo

Đề bài

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số \(y =  - \frac{{{x^2} + x + 1}}{x}\).

b) Tìm các giá trị của m để đường thẳng \(d:y =  - 2x + m\) cắt đồ thị (C) tại hai điểm phân biệt A và B thuộc hai nhánh của đồ thị và đoạn AB ngắn nhất.

Lời giải chi tiết

a) Tập xác định: \(\mathbb{R}\backslash \left\{ 0 \right\}\).

Sự biến thiên:

Ta có \(y =  - x - 1 - \frac{1}{x} \Rightarrow y' =  - 1 + \frac{1}{{{x^2}}} = \frac{{1 - {x^2}}}{{{x^2}}} \Rightarrow y' = 0 \Leftrightarrow \frac{{1 - {x^2}}}{{{x^2}}} = 0 \Leftrightarrow x =  \pm 1\) suy ra hàm số đồng biến trên từng khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\), nghịch biến trên từng khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).

Đồ thị hàm số có điểm cực đại là \(\left( {1; - 3} \right)\) và điểm cực tiểu là \(\left( { - 1;1} \right)\).

Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to  + \infty } y =  - \infty \), \(\mathop {\lim }\limits_{x \to  - \infty } y =  + \infty \);  \(\mathop {\lim }\limits_{x \to  \pm \infty } \left[ {y - \left( { - x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to  \pm \infty } \frac{{ - 1}}{x} = 0\) suy ra đường thẳng \(y = 2\) là tiệm cận xiên của đồ thị hàm số; \(\mathop {\lim }\limits_{x \to {0^ - }} y =  + \infty \), \(\mathop {\lim }\limits_{x \to {0^ + }} y =  - \infty \) suy ra trục tung là tiệm cận đứng của đồ thị hàm số.

Ta có bảng biến thiên:

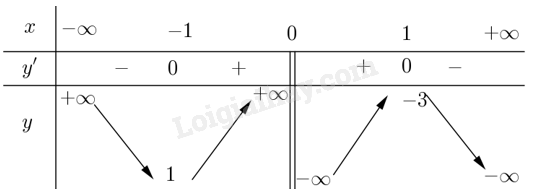
Đồ thị hàm số:

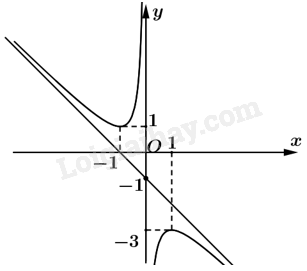
Đồ thị nhận điểm \(I\left( {0; - 1} \right)\) làm tâm đối xứng.

b) Xét phương trình hoành độ giao điểm của d và (C):

\( - 2x + m = \frac{{{x^2} + x + 1}}{x} \Leftrightarrow {x^2} - \left( {1 + m} \right)x - 1 = 0{\rm{ }}\left( {x \ne 0} \right).\left( 1 \right)\).

Đường thẳng d luôn cắt đồ thị hàm số (C) tại hai điểm phân biệt do phương trình (1) luôn có hai nghiệm trái dấu vì \(ac =  - 1 < 0\). Khi đó với \({x_1},{x_2}\) là hai nghiệm phân biệt của (1) thì ta có thể giả sử \(A\left( {{x_1}; - 2{x_1} + m} \right)\) và \(B\left( {{x_2}; - 2{x_2} + m} \right)\).

Ta có \(A{B^2} = {\left( {{x_1} - {x_2}} \right)^2} + {\left[ {\left( { - 2{x_1} + m} \right) - \left( { - 2{x_2} + m} \right)} \right]^2} = 5\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \right]\)

\( = 5\left[ {{{\left( {1 + m} \right)}^2} + 4} \right] \ge 20\forall m.\) Dấu “=” xảy ra khi \(m =  - 1\).

Vậy AB ngắn nhất khi \(m =  - 1\).