Giải bài 26 trang 52 sách bài tập toán 12 - Kết nối tri thức — Không quảng cáo

Đề bài

a) Lập bảng biến thiên của hàm số $y = \frac{{{x^2}}}{{x + 1}}$.

b) Tìm các giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $M = \frac{{{{\cos }^2}\alpha }}{{\cos \alpha  + 1}}$.

Lời giải chi tiết

a) Tập xác định: $\mathbb{R}\backslash \left\{ { - 1} \right\}$.

Ta có $y' = \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}} \Rightarrow y' = 0 \Leftrightarrow \frac{{{x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}} = 0 \Leftrightarrow x =  - 2$ hoặc $x = 0$.

Ta có bảng biến thiên:

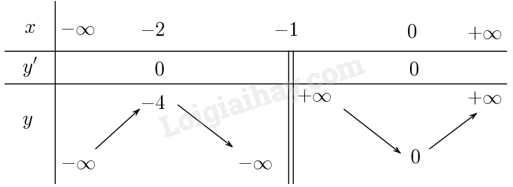
b) Đặt $x = \cos \alpha$, ta có $M = \frac{{{x^2}}}{{x + 1}},x \in \left( { - 1;1} \right]$.

Dựa vào bảng biến thiên ta có $\min M = \mathop {\min }\limits_{\left( { - 1;1} \right]} \frac{{{x^2}}}{{x + 1}} = 0$ và $\max M = \mathop {\max }\limits_{\left( { - 1;1} \right]} \frac{{{x^2}}}{{x + 1}} = y\left( 1 \right) = \frac{1}{2}$.