Giải bài 27 trang 52 sách bài tập toán 12 - Kết nối tri thức
Một hình chóp tứ giác đều ngoại tiếp hình cầu bán kính R. a) Chứng minh thể tích khối chóp tương ứng là (V = frac{{4{R^2}{x^2}}}{{3left( {x - 2R} right)}}), trong đó x là chiều cao hình chóp. b) Với giá trị nào của x để khối chóp tương ứng có thể tích nhỏ nhất?
Đề bài
Một hình chóp tứ giác đều ngoại tiếp hình cầu bán kính R.
a) Chứng minh thể tích khối chóp tương ứng là \(V = \frac{{4{R^2}{x^2}}}{{3\left( {x - 2R} \right)}}\), trong đó x là chiều cao hình chóp.
b) Với giá trị nào của x để khối chóp tương ứng có thể tích nhỏ nhất?
Phương pháp giải - Xem chi tiết
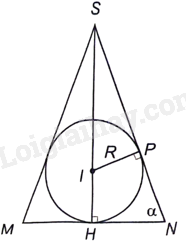
Ý a: Mặt phẳng đi qua đường cao SH của hình chóp và trung điểm M của một cạnh đáy
cắt hình chóp cắt hình chóp theo tam giác cân SMN và cắt hình cầu theo hình tròn tâm I bán kính R nội tiếp tam giác SMN. Có thể tính thể tích khối chóp theo x và \(\alpha = \widehat {SNH}\). Sauđó sử dụng đẳng thức \(x = R + IS\) để tìm hệ thức giữa R, x, \(\alpha \).
Ý b: Tìm giá trị nhỏ nhất của \(V = \frac{{4{R^2}{x^2}}}{{3\left( {x - 2R} \right)}}\).
Lời giải chi tiết
a) Ta có \(HN = x\cot \alpha ;MN = 2x\cot \alpha \).
Thể tích khối chóp là \(V = \frac{1}{3}M{N^2} \cdot SH = \frac{4}{3}{x^3}{\cot ^2}\alpha \). Ta tính \({\cot ^2}\alpha \) theo R và x.
Từ đẳng thức \(SH = IH + IS\) ta có \(x = R + \frac{R}{{\cos \alpha }}\). Do đó \(\cos \alpha = \frac{R}{{x - R}}\) suy ra
\({\sin ^2}\alpha = 1 - {\cos ^2}\alpha = 1 - \frac{{{R^2}}}{{{{\left( {x - R} \right)}^2}}} = \frac{{{x^2} - 2Rx}}{{{{\left( {x - R} \right)}^2}}};{\cot ^2}\alpha = \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{R^2}}}{{x\left( {x - 2R} \right)}}\)
Từ đó ta được \(V = \frac{{4{R^2}{x^2}}}{{3\left( {x - 2R} \right)}}\).
b) Xét hàm số \(f\left( x \right) = \frac{{4{R^2}{x^2}}}{{3\left( {x - 2R} \right)}},x > 2R\).
Ta có bảng biến thiên
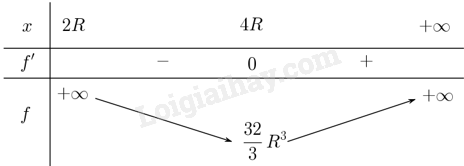
Dựa vào bảng biến thiên ta có \(\min V = \frac{{32}}{3}{R^3}\) khi \(x = 4R\).