Giải bài 3.4 trang 45 Chuyên đề học tập Toán 10 - Kết nối tri thức với cuộc sống
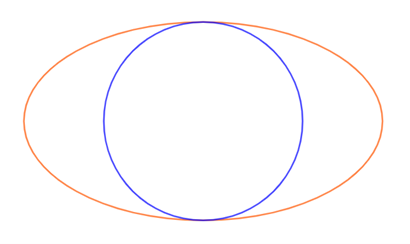
Đường tròn phụ của hình elip là đường tròn có đường kính là trục nhỏ của elip (H.3.8).
Đề bài
Đường tròn phụ của hình elip là đường tròn có đường kính là trục nhỏ của elip (H.3.8). Do đó, đường tròn phụ là đường tròn lớn nhất có thể nằm bên trong một hình elip. Tìm phương trình đường tròn phụ của elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) và chứng minh rằng, nếu điểm \(M({x_0};{y_0})\) thuộc elip thì điểm \(N(\frac{b}{a}{x_0};{y_0})\) thuộc đường tròn phụ.
Lời giải chi tiết
PTCT của elip là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
\( \Rightarrow \) Độ dài trục nhỏ là 2b.
Đường tròn phụ tâm O(0;0), đường kính 2b là: \({x^2} + {y^2} = {b^2}\)
Nếu \(M({x_0};{y_0})\) thuộc elip thì \(\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1 \Leftrightarrow \frac{{{b^2}}}{{{a^2}}}{x_0}^2 + {y_0}^2 = {b^2}\) hay \({\left( {\frac{b}{a}{x_0}} \right)^2} + {y_0}^2 = {b^2}\)
\( \Rightarrow \) \(N(\frac{b}{a}{x_0};{y_0})\) thuộc đường tròn phụ.