Giải bài 3 trang 68 sách bài tập toán 11 - Chân trời sáng tạo tập 2 — Không quảng cáo

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’. Tính khoảng cách giữa hai đường thẳng MN và B’D’.

Lời giải chi tiết

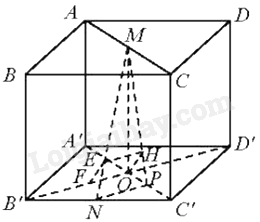
Gọi O là giao điểm của B’D’ và A’C’. Gọi P là trung điểm của OC’.

Vẽ $OH \bot MP,HE//NP,EF//OH$ (H thuộc MP, E thuộc MN, F thuộc B’D’)

Chứng minh được $B'D' \bot \left( {A'C'CA} \right)$ nên $B'D' \bot OH$, mà $EF//OH$ nên $EF \bot B'D'\left( 1 \right)$

Vì NP//B’D’ nên $NP \bot \left( {A'C'CA} \right) \Rightarrow NP \bot OH$, mà $OH \bot MP$ nên $OH \bot \left( {MNP} \right)$ hay $OH \bot MN$, mà $EF//OH$$\Rightarrow EF \bot MN\left( 2 \right)$

Từ (1) và (2) ta có: $d\left( {MN,B'D'} \right) = EF = OH$

Tam giác MOP vuông tại O, ta có: $OM = a,OP = \frac{1}{2}OC' = \frac{1}{4}A'C' = \frac{{a\sqrt 2 }}{4}$ nên

$\frac{1}{{O{H^2}}} = \frac{1}{{O{P^2}}} + \frac{1}{{O{M^2}}} = {\left( {\frac{4}{{a\sqrt 2 }}} \right)^2} + \frac{1}{{{a^2}}} = \frac{9}{{{a^2}}}$$\Rightarrow OH = \frac{a}{3}$