Giải bài 30 trang 100 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Cho hình chóp $S.ABCD$ có $AC$ cắt $BD$ tại $O$. Gọi $\alpha$, $\beta$ lần lượt là số đo của các góc nhị diện $\left[ {A,SO,B} \right]$ và $\left[ {B,SO,C} \right]$. Tính $\alpha  + \beta$.

Lời giải chi tiết

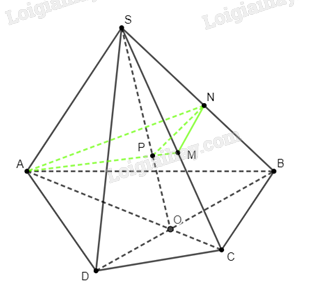
Gọi $P$ là hình chiếu của $A$ trên $SO$. Trên $\left( {SAC} \right)$, gọi $M$ là giao điểm của $SC$ và $AP$. Trên $\left( {SBD} \right)$, kẻ $NP \bot SO$ với $N \in SB$.

Dễ thấy rằng 4 điểm $A$, $P$, $M$, $N$ đồng phẳng.

Vì $AP \bot SO$, $NP \bot SO$ nên góc $\widehat {APN}$ là góc phẳng nhị diện của góc nhị diện $\left[ {A,SO,B} \right]$, tức là $\alpha  = \widehat {APN}$.

Chứng minh tương tự, ta có $\beta  = \widehat {NPM}$

Suy ra $\alpha  + \beta  = \widehat {APN} + \widehat {NPM} = \widehat {APM}$. Mặt khác, do $A$, $P$, $M$ thẳng hàng, nên ta có $\widehat {APM} = {180^o}$.

Như vậy $\alpha  + \beta  = {180^o}$.