Giải bài 36 trang 23 sách bài tập toán 9 - Cánh diều tập 1
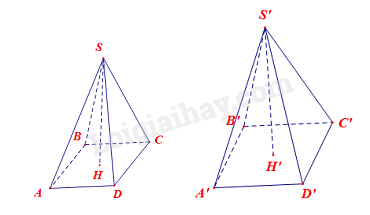
Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S’.A’B’C’D’ có cùng chiều cao SH= S’H = 30 cm. Thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S’A’B’C’D' là 240 cm3. Tính độ dài cạnh đáy của mỗi hình chóp, biết \(A'B' - AB = 2\)cm.
Đề bài
Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S’.A’B’C’D’ có cùng chiều cao SH= S’H = 30 cm. Thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S’A’B’C’D' là 240 cm 3 . Tính độ dài cạnh đáy của mỗi hình chóp, biết \(A'B' - AB = 2\)cm.
Phương pháp giải - Xem chi tiết

Giải hệ gồm 2 phương trình trên ta tìm được độ dài cạnh đáy của mỗi hình chóp.
Lời giải chi tiết
Ta có AB và A’B’ lần lượt là độ dài cạnh đáy của hình chóp tứ giác đều S.ABCD và S’.A’B’C’D’.
Theo đề bài ta có \(A'B' - AB = 2\).
Thể tích hình chóp S.ABCD là \(\frac{1}{3}.A{B^2}.30\) cm 3 và hình chóp S’.A’B’C’D’ là \(\frac{1}{3}.A'B{'^2}.30\) cm 3 .
Do thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S’A’B’C’D' là 240 cm 3 nên ta có phương trình \(\frac{1}{3}.A'B{'^2}.30 - \frac{1}{3}.A{B^2}.30 = 240\) hay \(A'B{'^2} - A{B^2} = 24\).
Ta lập được hệ phương trình \(\left\{ \begin{array}{l}A'B' - AB = 2\left( 1 \right)\\A'B{'^2} - A{B^2} = 24\left( 2 \right)\end{array} \right.\)
Từ (1) suy ra \(A'B' = 2 + AB\) (3). Thế (3) vào (2) ta được:
\(\begin{array}{l}{\left( {2 + AB} \right)^2} - A{B^2} = 24\\4 + 4AB + A{B^2} - A{B^2} - 24 = 0\\4AB = 20\\AB = 5\end{array}\)
Thay \(AB = 5\) vào (1) ta có \(A'B' = 2 + 5 = 7\).
Vậy độ dài cạnh đáy của 2 hình chóp S.ABCD và S’.A’B’C’D’ lần lượt là 5cm và 7cm.