Giải bài 4.24 trang 49 sách bài tập toán 9 - Kết nối tri thức tập 1
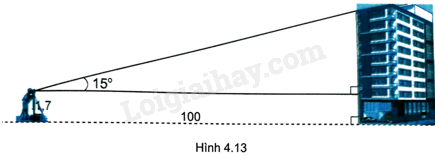
Một người đứng xa tòa nhà 100m, dùng giác kế thẳng đứng ngắm thấy điểm trên nóc nhà với góc nhìn ({15^o}) (so với phương nằm ngang) (H.4.13). Hỏi tòa nhà cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ nhất), biết chiều cao của giác kế là 1,7m?
Đề bài
Một người đứng xa tòa nhà 100m, dùng giác kế thẳng đứng ngắm thấy điểm trên nóc nhà với góc nhìn \({15^o}\) (so với phương nằm ngang) (H.4.13). Hỏi tòa nhà cao bao nhiêu mét (làm tròn đến chữ số thập phân thứ nhất), biết chiều cao của giác kế là 1,7m?
Phương pháp giải - Xem chi tiết
+ Gọi C là chân tòa nhà, D là điểm trên nóc tòa nhà, A là nơi đặt mắt giác kế, kẻ đường cao AH của tam giác ACD.
+ Tam giác AHD vuông tại H có: \(HD = AH.\tan \widehat {DAH}\).
+ Vì H ở giữa C và D nên \(CD = CH + HD\).
Lời giải chi tiết
Gọi C là chân tòa nhà, D là điểm trên nóc tòa nhà, A là nơi đặt mắt giác kế.
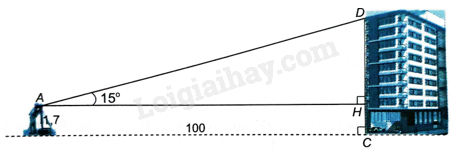
Kẻ đường cao AH của tam giác ACD nên
\(CH = 1,7m,AH = 100m,\widehat {DAH} = {15^o}\)
Tam giác AHD vuông tại H có:
\(HD = AH.\tan \widehat {DAH} = 100\tan {15^o}\left( m \right)\).
Vì H ở giữa C và D nên
\(CD = CH + HD = 1,7 + 100.\tan {15^o} \approx 28,5\left( m \right)\).