Giải bài 4.36 trang 53 sách bài tập toán 9 - Kết nối tri thức tập 1
Tìm độ dài dây cáp mắc giữa hai cọc ở vị trí C, D trên hai bên bờ vực như trong Hình 4.21 (làm tròn đến mét).
Đề bài
Tìm độ dài dây cáp mắc giữa hai cọc ở vị trí C, D trên hai bên bờ vực như trong Hình 4.21 (làm tròn đến mét).
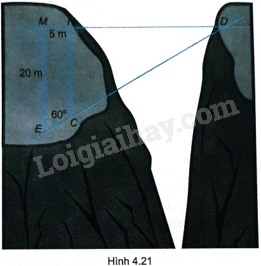
Phương pháp giải - Xem chi tiết
+ Theo kết quả bài 4.23: Cho hai điểm A, B. Nếu AN và PM cùng vuông góc MN, \(MN = n\), \(MP = p\), \(p > n\) và \(\widehat {MPA} = \alpha \) thì \(AB = \frac{{p\tan \alpha - n}}{{\sin \alpha }}\).
+ Thay \(p = 20m,n = 5m,\alpha = {60^o}\), \(\tan {60^o} = \sqrt 3 ;\sin {60^o} = \frac{{\sqrt 3 }}{2}\) ta có: \(CD = \frac{{20\sqrt 3 - 5}}{{\frac{{\sqrt 3 }}{2}}}\), từ đó tính được CD.
Lời giải chi tiết
Áp dụng bài tập 4.23 với \(p = 20m,n = 5m,\alpha = {60^o}\).
Do \(\tan {60^o} = \sqrt 3 ;\sin {60^o} = \frac{{\sqrt 3 }}{2}\)
suy ra \(CD = \frac{{20\sqrt 3 - 5}}{{\frac{{\sqrt 3 }}{2}}} \) \(= \frac{{2\left( {20\sqrt 3 - 5} \right)}}{{\sqrt 3 }} = \frac{{120 - 10\sqrt 3 }}{3} \approx 34\left( m \right)\)