Giải bài 4. 32 trang 52 sách bài tập toán 9 - Kết nối tri thức tập 1 — Không quảng cáo

Đề bài

Cho tam giác ABC có đường cao AH, $\widehat B = {60^o},\widehat C = {45^o}$ và cạnh $BC = 6cm$. Chứng minh rằng $AH = 3\left( {3 - \sqrt 3 } \right)cm$.

Lời giải chi tiết

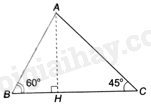
Tam giác ABC có góc B và góc C đều nhọn nên H nằm giữa B và C.

Tam giác ABH vuông tại H nên $AH = BH.\tan B = BH.\tan {60^o} = \sqrt 3 BH$,

suy ra $BH = \frac{{AH}}{{\sqrt 3 }}$.

Tam giác ACH vuông tại H có $\widehat C = {45^o}$ nên tam giác ACH vuông cân tại H nên $CH = AH$.

Ta có: $BC = BH + CH = AH\left( {\frac{1}{{\sqrt 3 }} + 1} \right)$ nên $\frac{{\sqrt 3  + 1}}{{\sqrt 3 }}AH = 6$,

suy ra $AH = \frac{{6\sqrt 3 }}{{\sqrt 3  + 1}} = 3\left( {3 - \sqrt 3 } \right)\left( {cm} \right)$