Giải bài 5.2 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho đường tròn (O) có bán kính bằng 2,5cm và hai tia Ox, Oy vuông góc với nhau tại O. Trên tia Ox lấy điểm A sao cho (OA = 3cm); trên tia Oy lấy điểm B sao cho (OB = 4cm). Gọi M là trung điểm của đoạn AB. Chứng minh rằng điểm M nằm trên đường tròn (O).
Đề bài
Cho đường tròn (O) có bán kính bằng 2,5cm và hai tia Ox, Oy vuông góc với nhau tại O. Trên tia Ox lấy điểm A sao cho \(OA = 3cm\); trên tia Oy lấy điểm B sao cho \(OB = 4cm\). Gọi M là trung điểm của đoạn AB. Chứng minh rằng điểm M nằm trên đường tròn (O).
Phương pháp giải - Xem chi tiết
+ Áp dụng định lí Pythagore vào tam giác AOB vuông tại O tính được AB.
+ Vì OM là đường trung tuyến của tam giác AOB vuông tại O nên: \(OM = \frac{1}{2}AB\), tính được OM, suy ra M nằm trên đường tròn (O).
Lời giải chi tiết
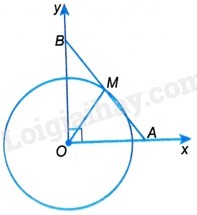
Áp dụng định lí Pythagore vào tam giác AOB vuông tại O ta có: \(A{B^2} = A{O^2} + O{B^2} = {3^2} + {4^2} = 25\) nên \(AB = 5cm\).
Vì OM là đường trung tuyến của tam giác AOB vuông tại O nên: \(OM = \frac{1}{2}AB = 2,5cm\).
Do đó, M nằm trên đường tròn (O).