Giải bài 4 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho parabol (P). Trên (P) lấy hai điểm M, N sao cho đoạn thẳng MN đi qua tiêu điểm F của (P). Chứng minh rằng khoảng cách từ trung điểm I của đoạn thẳng MN đến đường chuẩn  của (P) bằng \(\frac{1}{2}MN\) và đường tròn đường kính MN tiếp xúc với \(\Delta \).

Lời giải chi tiết

Gọi PTCT của parabol là \({y^2} = 2px\)

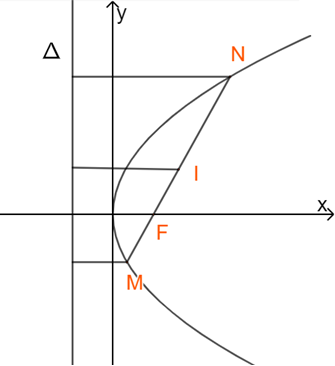
M, N nằm trên parabol nên ta có: \(d(M,\Delta ) = MF;d(N,\Delta ) = NF\)

\( \Rightarrow d\left( {I,\Delta } \right) = \frac{{d(M,\Delta ) + d(N,\Delta )}}{2} = \frac{{MF + NF}}{2} = \frac{{MN}}{2}\)