Giải bài 4 trang 60 SGK Toán 10 tập 1 – Cánh diều
Quan sát đồ thị hàm số bậc hai
Đề bài
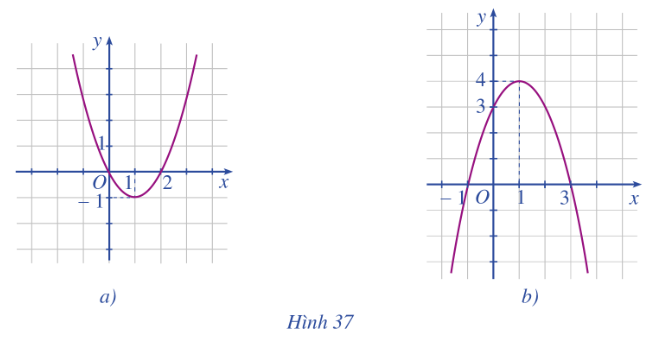
Quan sát đồ thị hàm số bậc hai \(y = a{x^2} + bx + c\) ở Hình 37a và Hình 37b rồi nêu:
a) Dấu của hệ số a;
b) Toạ độ đỉnh và trục đối xứng;
c) Khoảng đồng biến;
d) Khoảng nghịch biến;
e) Khoảng giá trị x mà y > 0;
g) Khoảng giá trị x mà \(y \le 0\).
Phương pháp giải - Xem chi tiết
a) Xác định bề lõm và so sánh a với 0
b) Xác định đỉnh và trục đối xứng của mỗi đồ thị.
c) Quan sát đồ thị và tìm khoảng đồng biến
d) Quan sát đồ thị và tìm khoảng nghịch biến
e) Khoảng giá trị x mà đồ thị nằm trên trục Ox
g) Khoảng giá trị x mà đồ thị nằm dưới trục Ox
Lời giải chi tiết
a)
Hình 37a: Bề lõm hướng lên trên nên a>0
Hình 37b: Bề lõm xuống nên a<0
b)
Hình 37a: Đỉnh là (1;-1), trục đối xứng x=1
Hình 37b: Đỉnh là (1;4), trục đối xứng x=1
c)
Hình 37a: Hàm số đồng biến trên \(\left( {1; + \infty } \right)\)
Hình 37b: Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\)
d)
Hình 37a: Hàm số nghịch biến trên \(\left( { - \infty ;1} \right)\)
Hình 37b: Hàm số nghịch biến trên \(\left( {1; + \infty } \right)\)
e)
Hình 37a: Đồ thị nằm trên trục Ox khi \(x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
=> Khoảng giá trị x mà y > 0 là \(\left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\)
Hình 37b: Đồ thị nằm trên trục Ox khi \(x \in \left( { - 1;3} \right)\)
=> Khoảng giá trị x mà y > 0 là \(\left( { - 1;3} \right)\)
g)
Hình 37a: Đồ thị nằm dưới trục Ox khi \(x \in \left[ {0;2} \right]\)
=> Khoảng giá trị x mà y < 0 là \(\left[ {0;2} \right]\)
Hình 37b: Đồ thị nằm dưới trục Ox khi \(x \in \left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)
=> Khoảng giá trị x mà \(y \le 0\) là \(\left( { - \infty ; - 1} \right] \cup \left[ {3; + \infty } \right)\)