Giải bài 51 trang 117 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Cho tứ diện $ABCD$ có $M$, $N$ lần lượt là trung điểm của các cạnh $AB$, $CD$. Xác định ảnh của tứ diện $ABCD$ qua phép chiếu song song có phương chiếu là đường thẳng $MN$, mặt phẳng chiếu là mặt phẳng $\left( Q \right)$ bất kì cắt đường thẳng $MN$.

Lời giải chi tiết

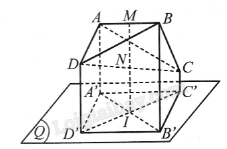
Gọi $f$ là phép chiếu song song có phương chiếu là đường thẳng $MN$, mặt phẳng chiếu là mặt phẳng $\left( Q \right)$ bất kì cắt $MN$.

Nhận xét rằng hình chiếu của song song của đoạn thẳng $MN$ theo phép chiếu $f$ là một điểm. Gọi điểm đó là $I$.

Gọi $A'$, $B'$, $C'$, $D'$ lần lượt là hình chiếu của $A$, $B$, $C$, $D$ theo phép chiếu $f$.

Do phép chiếu song song không làm thay đổi tỉ số giữa các đoạn thẳng cùng nằm trên 1 đường thẳng, nên do $M$ là trung điểm của $AB$ nên $I$ là trung điểm của $A'B'$. Tương tự, $I$ là trung điểm của $C'D'$. Suy ra $A'C'B'D'$ là hình bình hành.

Vậy hình chiếu của tứ diện $ABCD$ là hình bình hành $A'C'B'D'$ và hai đường chéo $A'B'$, $C'D'$ của nó.