Giải bài 6.16 trang 24 SGK Toán 10 – Kết nối tri thức
Giải các bất phương trình bậc hai:
Đề bài
Giải các bất phương trình bậc hai:
a) \({x^2} - 1 \ge 0\)
b) \({x^2} - 2x - 1 < 0\)
c) \( - 3{x^2} + 12x + 1 \le 0\)
d) \(5{x^2} + x + 1 \ge 0\)
Phương pháp giải - Xem chi tiết
Xét dấu tam thức bậc hai \(f(x) = a{x^2} + bx + c\)
Bước 1: Tính \(\Delta = {b^2} - 4ac\)
Bước 2:
- Nếu \(\Delta < 0\) thì \(f(x)\) luôn cùng dấu với a với mọi \(x \in \mathbb{R}\)
- Nếu \(\Delta = 0\) thì \(f(x)\)có nghiệm kép là \({x_0}\) . Vậy \(f(x)\)cùng dấu với a với \(x \ne {x_0}\)
- Nếu \(\Delta > 0\) thì \(f(x)\)có 2 nghiệm là \({x_1};{x_2}\)\(({x_1} < {x_2})\). Ta lập bảng xét dấu.

Lời giải chi tiết
a) Tam thức \(f(x) = {x^2} - 1\) có \(\Delta = 4 > 0\)nên f(x) có 2 nghiệm phân biệt \({x_1} = - 1;{x_2} = 1\)
Mặt khác a=1>0, do đó ta có bảng xét dấu:

Tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ {1; + \infty } \right)\)
b) Tam thức \(g(x) = {x^2} - 2x - 1\) có \(\Delta = 8 > 0\) nên g(x) có 2 nghiệm phân biệt \({x_1} = 1 - \sqrt 2 ;{x_2} = 1 + \sqrt 2 \)
Mặt khác a=1>0, do đó ta có bảng xét dấu:
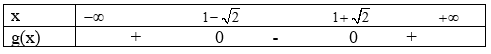
Tập nghiệm của bất phương trình là \(\left( {1 - \sqrt 2 ;1 + \sqrt 2 } \right)\)
c) Tam thức \(h(x) = - 3{x^2} + 12x + 1\) có\(\Delta ' = 39 > 0\)nên h(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - \sqrt {39} }}{3};{x_2} = \frac{{6 + \sqrt {39} }}{3}\)
Mặt khác a=-3<0, do đó ta có bảng xét dấu:

Tập nghiệm của bất phương trình là \(\left( { - \infty ; \frac{{6 - \sqrt {39} }}{3}} \right] \cup \left[ {\frac{{6 + \sqrt {39} }}{3}; + \infty } \right)\)
d) Tam thức \(k(x) = 5{x^2} + x + 1\) có \(\Delta = - 19 < 0\), hệ số a=5>0 nên k(x) luôn dương ( cùng dấu với a) với mọi x, tức là \(5{x^2} + x + 1 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm