Giải bài 6. 32 trang 65 SGK Toán 8 - Cùng khám phá — Không quảng cáo

Đề bài

Cho tam giác \(ABC\) có \(AH\) là đường cao và \(A{H^2} = BH.CH\). Chứng minh rằng:

a) Tam giác \(ABC\) đồng dạng với tam giác \(HBA\)

b) Tam giác \(ABC\) vuông tại A.

c) Cho \(BH = \frac{5}{{13}}\), Tính tỉ số chu vi và tỉ số diện tích của \(\Delta ABH\) và \(\Delta ABC\)

Lời giải chi tiết

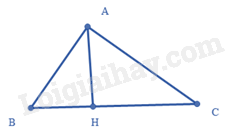
a) Ta có:

\(\begin{array}{l}A{H^2} = BH.CH\\AH.AH = BH.CH\\\frac{{AH}}{{BH}} = \frac{{CH}}{{AH}}\end{array}\)

Xét tam giác \(ABH\) và tam giác \(CAH\), ta có:

\(\frac{{AH}}{{BH}} = \frac{{CH}}{{AH}}\)

\(\widehat {BHA} = \widehat {AHC} = 90^\circ \) (do \(AH\) là đường cao)

=> \(\Delta ABH\)∽\(\Delta CAH\) (cạnh góc vuông-góc vuông)

b) Vì \(\Delta ABH\)∽\(\Delta CAH\), ta có tỉ lệ:

\(A{H^2} = BH.CH\)

Áp dụng hệ thức lượng trong tam giác vuông, suy ra tam giác \(ABC\) là tam giác vuông tại \(A\).

c) Ta có:

\(\begin{array}{l}BH = \frac{5}{{13}}AB\\ \Rightarrow \frac{{BH}}{{AB}} = \frac{5}{{13}}\end{array}\)

Dựa vào tỉ lệ trên ta có \(BH = 5;AB = 13\)

\( \Rightarrow AH = \sqrt {A{B^2} - B{H^2}}  = \sqrt {{{13}^2} - {5^2}}  = 12\)

Chu vi của tam giác \(ABH\) là: \(AB + BH + HA = 13 + 5 + 12 = 30\)

Diện tích của tam giác \(ABH\) là: \(\frac{1}{2}AH.BH = \frac{1}{2}.12.5 = 30\)

Xét tam giác \(ABC\) và tam giác \(HBA\), ta có:

\(\widehat A = \widehat {BHA} = 90^\circ \)

\(\widehat B\) là góc chung

=> \(\Delta ABC\)∽\(\Delta HBA\) (góc nhọn-góc vuông)

Ta có tỉ lệ:

\(\begin{array}{l}\frac{{AB}}{{BC}} = \frac{{AH}}{{AC}} = \frac{{HB}}{{AB}}\\\frac{{13}}{{BC}} = \frac{{12}}{{AC}} = \frac{5}{{13}}\\ \Rightarrow BC = 33,8;AC = 31,2\end{array}\)

Chu vi của tam giác \(ABC\) là: \(AB + BC + AC = 13 + 33,8 + 31,2 = 78\)

Diện tích của tam giác \(ABC\) là: \(\frac{1}{2}.AC.AB = \frac{1}{2}.31,2.13 = 202,8\)

Tỉ số chu vi của \(\Delta ABH\) và \(\Delta ABC\) là: \(\frac{{30}}{{78}} = \frac{5}{{13}}\)

Tỉ số diện tích của \(\Delta ABH\) và \(\Delta ABC\) là: \(\frac{{30}}{{202,8}} = \frac{{25}}{{169}}\)