Giải bài 6. 56 trang 22 sách bài tập toán 11 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

a) Vẽ đồ thị của hai hàm số $y = {e^x}$ và $y = {\rm{ln}}x$ trên cùng một hệ trục toạ độ.

b) Chứng minh rằng hai đồ thị trên đối xứng nhau qua đường thẳng $y = x$ tức điểm $M$ nằm trên một đồ thị thì $M'$ đối xứng với $M$ qua đường thẳng $y = x$ sẽ nằm trên đồ thị còn lại.

Lời giải chi tiết

a) Đồ thị của hai hàm số $y = {e^x}$ và $y = {\rm{ln}}x$ trên cùng một hệ trục toạ độ như hình sau:

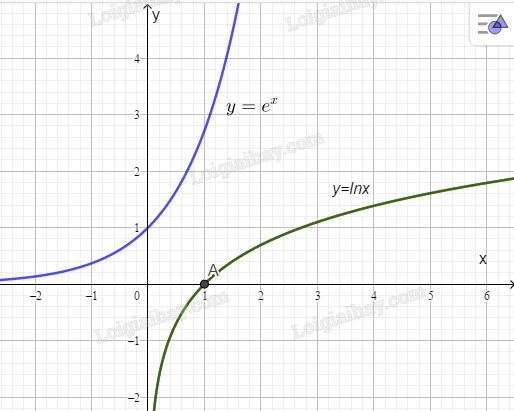
b) Xét điểm $A\left( {{x_0},{e^{{x_0}}}} \right)$ nằm trên đồ thị hàm số $y = {e^x}$.

Viết phương trình đường thằng đi qua $A$ vuông góc với đường thẳng $y = x$:

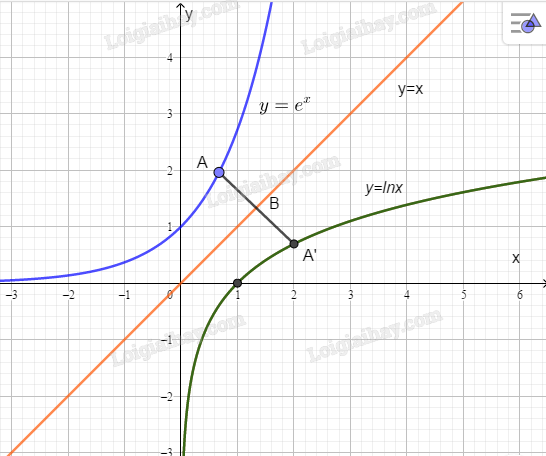
Toạ độ giao điểm của đường thẳng ${\rm{d}}$ và đường thẳng $y = x$ là $B\left( {\frac{{{x_0} + {e^{{x_0}}}}}{2};\frac{{{x_0} + {e^{{x_0}}}}}{2}} \right)$

Gọi $A'$ là điểm đối xứng của $A$ qua đường thằng $y = x$. Ta tìm được $A'\left( {{e^{{x_0}}};{x_0}} \right)$. Khi đó $A'$ thuộc đồ thị hàm số $y = {\rm{ln}}x$. Tương tự nếu điếm $B\left( {{x_0}{\rm{;ln}}{x_0}} \right)$ nằm trền đồ thị hàm số $y = {\rm{ln}}x$ thì ta cũng có thể tìm toạ độ của điềm $B'$ đối xứng với $B$ qua đường thẳng $y = x$ và chứng minh $B'$ thuộc đồ thị hàm số $y = {e^x}$.

Vậy hai đồ thị đã cho đối xứng với nhau qua đường thẳng $y = x$.

Chú ý: Tổng quát, có thề chứng minh rằng đồ thị của hai hàm số $y = {a^x}$ và $y = {\rm{lo}}{{\rm{g}}_a}x(0 < a \ne 1)$ đối xứng với nhau qua đường phân giác của góc phẩn tư thứ nhất (tức là đường thẳng $y = x$ ).