Giải bài 7. 46 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Cho hình chóp \(S.ABCD\)có tất cả các cạnh đều bằng a, gọi \(O\) là giao điểm của \(AC\)và\(BD\). Khoản cách từ điểm \(O\) đến mặt phẳng \(\left( {SBC} \right)\) bằng

A. \(\frac{{a\sqrt 6 }}{6}\).

B. \(\frac{{a\sqrt 3 }}{3}\).

C. \(\frac{{a\sqrt 3 }}{2}\).

D. \(\frac{{a\sqrt 6 }}{3}\).

Lời giải chi tiết

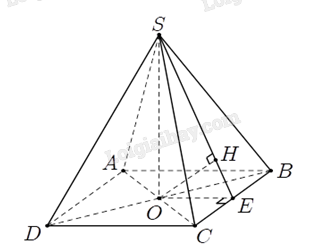
Tính khoảng cách từ \(O\) tới \(mp\left( {SBC} \right)\):

Gọi \(E\) là trung điểm của \(BC\).

Theo giả thiết \(SO \bot \left( {ABCD} \right) \supset BC\).

\( \Rightarrow \) \(\left\{ \begin{array}{l}BC \bot SO \subset \left( {SOE} \right)\\BC \bot OE \subset \left( {SOE} \right)\\OE \cap SO = O\end{array} \right.\) \( \Rightarrow \) \(BC \bot \left( {SOE} \right)\) mà \(BC \subset \left( {SBC} \right)\)\( \Rightarrow \) \(\left( {SBC} \right) \bot \left( {SOE} \right)\).

Gọi \(H\) là hình chiếu vuông góc của \(O\) lên \(SE\)\( \Rightarrow OH \bot SE = \left( {SBC} \right) \cap \left( {SOE} \right)\), suy ra \(OH \bot \left( {SBC} \right)\) nên \(d\left( {O,\left( {SBC} \right)} \right) = OH\).

Ta có \(SO = \sqrt {S{C^2} - O{C^2}}  = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}  = \frac{{a\sqrt 2 }}{2}\).

Trong \(\Delta SOE\) vuông tại \(O\), ta có:

\(\frac{1}{{O{H^2}}} = \frac{1}{{O{E^2}}} + \frac{1}{{O{S^2}}} = \frac{1}{{{{\left( {\frac{a}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}} = \frac{6}{{{a^2}}}\) \( \Rightarrow \) \(OH = \frac{a}{{\sqrt 6 }}\)

\( \Rightarrow \)\(d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{a}{{\sqrt 6 }} = \frac{{a\sqrt 6 }}{6}\).