Giải bài 72 trang 85 sách bài tập toán 8 – Cánh diều
Cho hình bình hành \(ABCD\left( AC>BD \right)\). Vẽ \(CE\) vuông góc với đường thẳng \(AB\) tại \(E,CF\) vuông góc với đường thẳng \(AD\) tại \(F,BH\) vuông góc với đường thẳng \(AC\) tại \(H\).
Đề bài
Cho hình bình hành \(ABCD\left( AC>BD \right)\). Vẽ \(CE\) vuông góc với đường thẳng \(AB\) tại \(E,CF\) vuông góc với đường thẳng \(AD\) tại \(F,BH\) vuông góc với đường thẳng \(AC\) tại \(H\). Chứng minh:
a) \(\Delta ABH\backsim \Delta ACE;\Delta CBH\backsim \Delta ACF\)
b) \(B{{H}^{2}}=HK.HQ\), biết tia \(BH\) cắt đường thẳng \(CD\) tại \(Q\); cắt cạnh \(AD\) tại \(K\).
Phương pháp giải - Xem chi tiết
Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu:
\(\widehat{A'}=\widehat{A},\widehat{B'}=\widehat{B},\widehat{C'}=\widehat{C}\) ; \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}\).
Kí hiệu là \(\Delta A'B'C'\backsim \Delta ABC\).
Tỉ số các cạnh tương ứng \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=k\) gọi là tỉ số đồng dạng.
Lời giải chi tiết
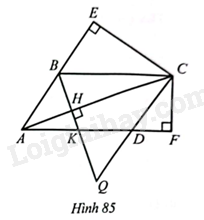
a) Ta có hai tam giác \(ABH\) và \(ACE\) đều là các tam giác vuông và \(\widehat{BAH}=\widehat{EAC}\). Suy ra \(\Delta ABH\backsim \Delta ACE\). Hai tam giác \(CBH\) và \(ACF\) đều là các tam giác vuông và \(\widehat{BCH}=\widehat{CAF}\) , suy ra \(\Delta CBH\backsim \Delta ACF\).
b) Do \(AB//CQ\) nên \(\frac{QH}{BH}=\frac{CH}{AH}\)
Lại có \(BC//AK\) nên \(\frac{BH}{HK}=\frac{CH}{AH}\)
Suy ra \(\frac{QH}{BH}=\frac{BH}{HK}\). Hay \(B{{H}^{2}}=HK.HQ\).