Giải bài 67 trang 85 sách bài tập toán 8 – Cánh diều
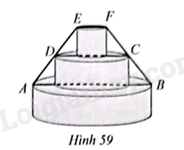
Một chiếc kệ bày hoa quả có ba tầng được thiết kế như Hình 59. Tầng đáy có đường kính \(AB\) là 32 cm.
Đề bài
Một chiếc kệ bày hoa quả có ba tầng được thiết kế như Hình 59. Tầng đáy có đường kính \(AB\) là 32 cm. Tầng giữa có đường kính \(CD\) nhỏ hơn đường kính tầng đáy là 12 cm. Tính độ dài đường kính tầng trên cùng \(EF\), biết \(EF//AB\); \(D,C\) lần lượt là trung điểm của \(EA\) và \(FB\).
Phương pháp giải - Xem chi tiết
Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu:
\(\widehat{A'}=\widehat{A},\widehat{B'}=\widehat{B},\widehat{C'}=\widehat{C}\) ; \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}\).
Kí hiệu là \(\Delta A'B'C'\backsim \Delta ABC\).
Tỉ số các cạnh tương ứng \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=k\) gọi là tỉ số đồng dạng.
Lời giải chi tiết
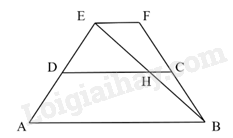
Tầng giữa có đường kính \(CD\) là: \(32-12=20\)cm.
Ta có: \(EF//AB;D,C\) lần lượt là trung điểm của \(EA\) và \(FB\)
\(=>DC//EF//AB\)
Xét hai tam giác \(EHD\) và \(EAB\) có \(DH//AB=>\Delta EHD\backsim \Delta EAB\)
$ =>\frac{DE}{AE}=\frac{DH}{AB}=\frac{1}{2} \\ =>DH=\frac{AB.DE}{AE}=\frac{32.1}{2}=16cm $
Độ dài \(HC=DC-DH=20-16=4\)cm.
Xét hai tam giác \(BHC\) và \(BEF\) có \(HC//EF=>\Delta BHC\backsim \Delta BEF\)
$ =>\frac{HC}{EF}=\frac{BC}{BF}=\frac{1}{2} \\=>EF=2.HC=2.4=8cm \\$
Vậy độ dài đường kính tầng trên cùng \(EF=8\)cm.