Giải bài 76 trang 107 SBT toán 10 - Cánh diều
Cho tam giác ABC có AB = 4, AC = 5, \(\widehat {BAC}\) = 120°. Điểm M là trung điểm của đoạn thẳng BC, điểm D thoả mãn \(\overrightarrow {AD} = \frac{2}{5}\overrightarrow {AC} \). Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \) và chứng minh \(AM \bot BD\)
Đề bài
Cho tam giác ABC có AB = 4, AC = 5, \(\widehat {BAC}\) = 120°. Điểm M là trung điểm của đoạn thẳng BC , điểm D thoả mãn \(\overrightarrow {AD} = \frac{2}{5}\overrightarrow {AC} \). Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \) và chứng minh \(AM \bot BD\)
Phương pháp giải - Xem chi tiết
Bước 1: Sử dụng định nghĩa tích vô hướng của hai vectơ để tính \(\overrightarrow {AB} .\overrightarrow {AC} \)
Bước 2: Sử dụng tích chất trung điểm của đoạn thẳng và tách các vectơ rồi sử dụng định nghĩa tích vô hướng của hai vectơ để biến đổi tích vô hướng \(\overrightarrow {AM} .\overrightarrow {BD} \)
Bước 3: Chứng minh \(\overrightarrow {AM} .\overrightarrow {BD} = 0\)rồi kết luận
Lời giải chi tiết
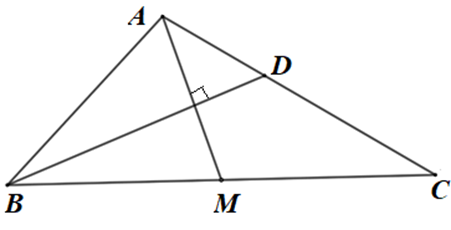
a) Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = 4.5.\cos {120^0} = - 10\)
b) Do M là trung điểm BC nên \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\); \(AD = \frac{2}{5}AC = 2\)
Xét \(\overrightarrow {AM} .\overrightarrow {BD} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)\)\( = \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AD} - \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AD} - \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AB} \)
\( = \frac{1}{2}AB.AD.\cos \widehat {BAD} - \frac{1}{2}A{B^2} + \frac{1}{2}.\frac{2}{5}A{C^2} - \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AC} \)
\( = \frac{1}{2}.4.2.\cos {120^0} - \frac{1}{2}{.4^2} + \frac{1}{5}{.5^2} - \frac{1}{2}.( - 10) = 0\)
\( \Rightarrow \overrightarrow {AM} .\overrightarrow {BD} = 0 \Rightarrow AM \bot BD\)