Giải bài 77 trang 107 SBT toán 10 - Cánh diều
Một người quan sát đứng ở bờ sông muốn đo độ rộng của khúc sông chỗ chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ song song
Đề bài
Một người quan sát đứng ở bờ sông muốn đo độ rộng của khúc sông chỗ chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ song song với nhau).
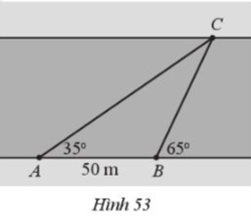
Từ vị trí đang đứng A , người đó đo được góc nghiêng \(\alpha \) = 35° so với bờ sông tới một vị trí C quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí B cách A một khoảng d = 50 m và tiếp tục đo được góc nghiêng \(\beta \)=65° so với bờ sông tới vị trí C đã chọn (Hình 53). Hỏi độ rộng của con sông chỗ chảy qua vị trí người quan sát đang đứng là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải - Xem chi tiết
Độ rộng khúc sông là chiều cao kẻ từ đỉnh C của ∆ ABC
Bước 1: Tính góc \(\widehat {ABC},\widehat {ACB}\)
Bước 2: Sử dụng định lí sin để tính độ dài BC của ∆ ABC
Bước 3: Tính diện tích tam giác ABC theo công thức \(S = \frac{1}{2}BC.AB.\sin \widehat {ABC}\)
Bước 4: Tính chiều cao h C của tam giác ABC theo công thức \(S = \frac{1}{2}AB.{h_C}\) rồi kết luận
Lời giải chi tiết
Ta có: \(\widehat {ABC} = {180^0} - {65^0} = {115^0} \Rightarrow \widehat {ACB} = {180^0} - \left( {\widehat {CAB} + \widehat {ABC}} \right) = {30^0}\)
Áp dụng định lí sin cho ∆ ABC ta có: \(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}} \Rightarrow BC = \frac{{AB.\sin A}}{{\sin C}} = \frac{{50.\sin {{35}^0}}}{{\sin {{30}^0}}} \approx 57,36\) (m)
Diện tích tam giác ABC là: \(S = \frac{1}{2}BC.AB.\sin \widehat {ABC} = \frac{1}{2}.57,36.50.\sin {115^0} \approx 1299,65\) (m 2 )
Gọi h c là chiều cao kẻ từ đỉnh C của ∆ ABC
Ta có: \(S = \frac{1}{2}AB.{h_C} \Rightarrow {h_C} = \frac{{2S}}{{AB}} \approx 51,99\) (m)
Vậy chiều rộng khúc sông là 51,99 m