Giải bài 79 trang 108 SBT toán 10 - Cánh diều — Không quảng cáo

Đề bài

a) Chứng minh đẳng thức ${\left| {\overrightarrow a  + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b$ với $\overrightarrow a ,\overrightarrow b$ là hai vectơ bất kì

b) Cho $\left| {\overrightarrow a } \right| = 2,\left| {\overrightarrow b } \right| = 3,\left| {\overrightarrow a  + \overrightarrow b } \right| = \sqrt 7$. Tinh $\overrightarrow a .\overrightarrow b$ và $\left( {\overrightarrow a ,\overrightarrow b } \right)$

Lời giải chi tiết

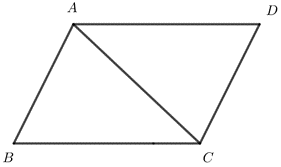
a) Xét hình bình hành ABCD thỏa mãn $\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {AD}  = \overrightarrow b$

Theo quy tắc hình bình hành ta có:

$\overrightarrow a  + \overrightarrow b  = \overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC}  \Rightarrow \left| {\overrightarrow a  + \overrightarrow b } \right| = AC$

Mà $A{C^2} = A{B^2} + B{C^2} - 2AB.AC.\cos B = A{B^2} + A{D^2} - 2AB.AD.\cos B$

Mặt khác, $\widehat {BAD} + \widehat B = {180^0} \Rightarrow \cos \widehat B =  - \cos \widehat {BAD}$

$\Rightarrow A{C^2} = A{B^2} + A{D^2} + 2AB.AD.\cos \widehat {BAD} = {\left| {\overrightarrow {AB} } \right|^2} + {\left| {\overrightarrow {AD} } \right|^2} + 2AB.AD.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = {\left| {\overrightarrow {AB} } \right|^2} + {\left| {\overrightarrow {AD} } \right|^2} + 2\overrightarrow {AB} .\overrightarrow {AD}$

$\Rightarrow {\left| {\overrightarrow a  + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b$ (ĐPCM)

b) Theo a) ${\left| {\overrightarrow a  + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b$

$\Rightarrow \overrightarrow a .\overrightarrow b  = \frac{{{{\left| {\overrightarrow a  + \overrightarrow b } \right|}^2} - {{\left| {\overrightarrow a } \right|}^2} - {{\left| {\overrightarrow b } \right|}^2}}}{2} = \frac{{{{\sqrt 7 }^2} - {2^2} - {3^2}}}{2} =  - 3$

Ta có: $\overrightarrow a .\overrightarrow b  =  - 3 \Leftrightarrow \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) =  - 3 \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{ - 3}}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} =  - \frac{1}{2}$ $\Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {120^0}$