Giải bài 80 trang 108 SBT toán 10 - Cánh diều — Không quảng cáo

Đề bài

Cho tam giác ABC có ba trung tuyến AD , BE , CF . Chứng minh rằng:

$\overrightarrow {AD} .\overrightarrow {BC}  + \overrightarrow {BE} .\overrightarrow {CA}  + \overrightarrow {CF} .\overrightarrow {AB}  = 0$(*)

Lời giải chi tiết

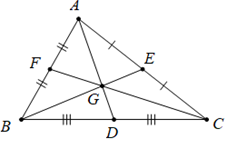
+ Do D là trung điểm BC nên $\overrightarrow {AD}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)$

+ Do E là trung điểm AC nên $\overrightarrow {BE}  = \frac{1}{2}\left( {\overrightarrow {BA}  + \overrightarrow {BC} } \right)$

+ Do F là trung điểm AB nên $\overrightarrow {CF}  = \frac{1}{2}\left( {\overrightarrow {CA}  + \overrightarrow {CB} } \right)$

Ta có: $\overrightarrow {AD} .\overrightarrow {BC}  + \overrightarrow {BE} .\overrightarrow {CA}  + \overrightarrow {CF} .\overrightarrow {AB}$$= \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right).\overrightarrow {BC}  + \frac{1}{2}\left( {\overrightarrow {BA}  + \overrightarrow {BC} } \right).\overrightarrow {CA}  + \frac{1}{2}\left( {\overrightarrow {CA}  + \overrightarrow {CB} } \right).\overrightarrow {AB}$

$= \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {BC}  + \overrightarrow {AC} .\overrightarrow {BC}  + \overrightarrow {BA} .\overrightarrow {CA}  + \overrightarrow {BC} .\overrightarrow {CA}  + \overrightarrow {CA} .\overrightarrow {AB}  + \overrightarrow {CB} .\overrightarrow {AB} } \right)$

$= \frac{1}{2}\left( { - \overrightarrow {BA} .\overrightarrow {BC}  + \overrightarrow {CA} .\overrightarrow {CB}  + \overrightarrow {AB} .\overrightarrow {AC}  - \overrightarrow {CB} .\overrightarrow {CA}  - \overrightarrow {AC} .\overrightarrow {AB}  + \overrightarrow {BC} .\overrightarrow {BA} } \right)$$= \frac{1}{2}.0 = 0$ (ĐPCM)