Giải bài 8 trang 105, 106 vở thực hành Toán 9 tập 2
Cho ngũ giác đều ABCDE có các cạnh bằng 4cm nội tiếp một đường tròn (O). a) Tính bán kính của (O) biết rằng ta lấy (cos {54^o} approx 0,59). b) Liệt kê năm phép quay ngược chiều giữ nguyên ngũ giác đều ABCDE.
Đề bài
Cho ngũ giác đều ABCDE có các cạnh bằng 4cm nội tiếp một đường tròn (O).
a) Tính bán kính của (O) biết rằng ta lấy \(\cos {54^o} \approx 0,59\).
b) Liệt kê năm phép quay ngược chiều giữ nguyên ngũ giác đều ABCDE.
Phương pháp giải - Xem chi tiết
a) + Nhận thấy $\overset\frown{AB}=\overset\frown{BC}=\overset\frown{CD}=\overset\frown{DE}=\overset\frown{EA}$, từ đó tính được góc AOB.
+ Gọi M là trung điểm của AB. Chứng minh OM vuông góc với AB và OM là tia phân giác của góc AOB, từ đó tính được góc AOM và góc MAO.
+ Bán kính của (O) là \(R = \frac{{AM}}{{\cos \widehat {MAO}}}\).
b) Phép quay ngược chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
Lời giải chi tiết
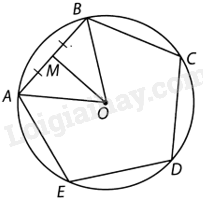
a) Ta thấy các cung nhỏ sau thỏa mãn: $\overset\frown{AB}=\overset\frown{BC}=\overset\frown{CD}=\overset\frown{DE}=\overset\frown{EA}$. Suy ra $\widehat{AOB}=sđ\overset\frown{AB}=\frac{{{360}^{o}}}{5}={{72}^{o}}$.
Gọi M là trung điểm của AB. Vì tam giác AOB cân tại O nên OM vuông góc với AB và OM là tia phân giác của góc AOB. Suy ra: \(\widehat {AOM} = \frac{{\widehat {AOB}}}{2} = \frac{{{{72}^o}}}{2} = {36^o}\).
Như vậy \(\widehat {MAO} = {90^o} - \widehat {AOM} = {54^o}\)
Bán kính của (O) là: \(R = \frac{{AM}}{{\cos \widehat {MAO}}} = \frac{{AM}}{{\cos {{54}^o}}} \approx \frac{2}{{0,59}} \approx 3,39\left( {cm} \right)\).
b) Năm phép quay ngược chiều giữ nguyên ngũ giác đều là các phép quay ngược chiều lần lượt \({72^{\rm{o}}},\,\,{144^{\rm{o}}},\) \({216^{\rm{o}}},\,\,{288^{\rm{o}}},\,\,{360^{\rm{o}}}\) với tâm O.