Giải bài 8 trang 118, 119 vở thực hành Toán 9 tập 2
Tam giác ABC cân tại A, đường cao AH, có (AB = 5cm,BC = 8cm). Quay tam giác ABC một vòng quanh cạnh AH ta được một hình nón. a) Tính thể tích của hình nón (làm tròn kết quả đến hàng phần trăm của (c{m^3})). b) Tính diện tích toàn phần của hình nón (làm tròn kết quả đến hàng phần trăm của (c{m^2})).
Đề bài
Tam giác ABC cân tại A, đường cao AH, có \(AB = 5cm,BC = 8cm\). Quay tam giác ABC một vòng quanh cạnh AH ta được một hình nón.
a) Tính thể tích của hình nón (làm tròn kết quả đến hàng phần trăm của \(c{m^3}\)).
b) Tính diện tích toàn phần của hình nón (làm tròn kết quả đến hàng phần trăm của \(c{m^2}\)).
Phương pháp giải - Xem chi tiết
a) Thể tích của hình nón có bán kính đáy R và chiều cao h là: \(V={{S}_{đ\acute{a}y}}.h=\pi {{R}^{2}}h\).
b) Diện tích xung quanh của hình nón bán kính r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).
Diện tích toàn phần hình nón bằng diện tích xung quanh cộng với diện tích hai đáy.
Lời giải chi tiết
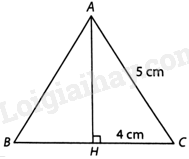
a) Tam giác ABC cân tại A, đường cao AH. Suy ra H là trung điểm của BC nên \(HC = HB = \frac{{BC}}{2} = 4cm\)
Tam giác AHC vuông tại H nên theo định lí Pythagore ta có:
\(A{H^2} + H{C^2} = A{C^2}\)
\(A{H^2} + {4^2} = {5^2}\)
\(A{H^2} = 25 - 16 = 9\)
\(AH = 3cm\).
Khi đó: \(R = 4cm,h = 3cm,l = 5cm\)
Thể tích của hình nón là: \(V=\frac{1}{3}{{S}_{đ\acute{a}y}}.h=\frac{1}{3}\pi {{R}^{2}}h=\frac{1}{3}\pi {{.4}^{2}}.3=16\pi \approx 50,27\left( c{{m}^{3}} \right)\)
b) Diện tích toàn phần của hình nón là: \({{S}_{tp}}={{S}_{xq}}+{{S}_{đ\acute{a}y}}=\pi Rl+\pi {{R}^{2}}=\pi .4.5+\pi {{.4}^{2}}=36\pi \approx 113,10\left( c{{m}^{2}} \right)\)