Giải bài 8 trang 22 sách bài tập toán 12 - Chân trời sáng tạo
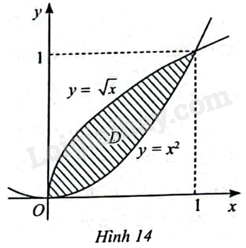
Gọi (D) là hình phẳng giới hạn bởi đồ thị của hai hàm số (y = {x^2}) và (y = sqrt x ) (Hình 14). a) Tính diện tích của (D). b) Tinh thể tích của khối tròn xoay tạo thành khi quay (D) quanh trục (Ox).
Đề bài
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2}\) và \(y = \sqrt x \) (Hình 14).
a) Tính diện tích của \(D\).
b) Tinh thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
‒ Sử dụng công thức: Tính thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\) quay quanh trục \(Ox\) là: \(V = \pi \int\limits_a^b {\left| {{{\left[ {f\left( x \right)} \right]}^2} - {{\left[ {g\left( x \right)} \right]}^2}} \right|dx} \).
Lời giải chi tiết
a) \(S = \int\limits_0^1 {\left| {\sqrt x - {x^2}} \right|dx} = \int\limits_0^1 {\left( {\sqrt x - {x^2}} \right)dx} = \int\limits_0^1 {\left( {{x^{\frac{1}{2}}} - {x^2}} \right)dx} = \left. {\left( {\frac{2}{3}{x^{\frac{3}{2}}} - \frac{{{x^3}}}{3}} \right)} \right|_0^1 = \frac{1}{3}\).
b) \(V = \pi \int\limits_0^1 {\left| {{{\left( {\sqrt x } \right)}^2} - {{\left( {{x^2}} \right)}^2}} \right|dx} = \pi \int\limits_0^1 {\left| {x - {x^4}} \right|dx} \)
\(x - {x^4} = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = 1\).
\(V = \pi \int\limits_0^1 {\left| {x - {x^4}} \right|dx} = \left| {\pi \int\limits_0^1 {\left( {x - {x^4}} \right)dx} } \right| = \left| {\left. {\pi \left( {\frac{{{x^2}}}{2} - \frac{{{x^5}}}{5}} \right)} \right|_0^1} \right| = \frac{{3\pi }}{{10}}\).