Giải bài 9.23 trang 55 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường chéo AC và BD cắt nhau tại điểm E. Tính số đo các góc của tứ giác ABCD, biết rằng (widehat {AEB} = {80^o},widehat {ABE} = {70^o}) và (widehat {ECB} = {50^o}).
Đề bài
Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường chéo AC và BD cắt nhau tại điểm E. Tính số đo các góc của tứ giác ABCD, biết rằng \(\widehat {AEB} = {80^o},\widehat {ABE} = {70^o}\) và \(\widehat {ECB} = {50^o}\).
Phương pháp giải - Xem chi tiết
+ \(\widehat {BAE} = {180^o} - \widehat {AEB} - \widehat {ABE}\).
+ Ta có: \(\widehat {ACD} = \widehat {ABE} = {70^o}\),
\(\widehat {ADB} = \widehat {ECB} = {50^o}\),
\(\widehat {CDB} = \widehat {BAC} = {30^o}\).
+ \(\widehat {BCD} = \widehat {ECB} + \widehat {ACD} = {120^o},\)
\(\widehat {CDA} = \widehat {CDB} + \widehat {ADB} = {80^o}\).
+ Vì tứ giác ABCD nội tiếp đường tròn (O) nên \(\widehat {DAB} = {180^o} - \widehat {BCD},\widehat {ABC} = {180^o} - \widehat {CDA}\).
Lời giải chi tiết
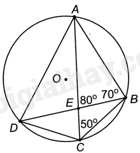
a) Tam giác ABE có: \(\widehat {BAE} = {180^o} - \widehat {AEB} - \widehat {ABE} = {30^o}\).
Xét đường tròn (O):
+ \(\widehat {ACD} = \widehat {ABE} = {70^o}\) (hai góc nội tiếp cùng chắn cung nhỏ AD).
+ \(\widehat {ADB} = \widehat {ECB} = {50^o}\) (hai góc nội tiếp cùng chắn cung nhỏ AB).
+ \(\widehat {CDB} = \widehat {BAC} = {30^o}\) (hai góc nội tiếp cùng chắn cung nhỏ CB).
Ta có:
\(\widehat {BCD} = \widehat {ECB} + \widehat {ACD} = {120^o},\\\widehat {CDA} = \widehat {CDB} + \widehat {ADB} = {80^o}.\)
Vì tứ giác ABCD nội tiếp đường tròn (O) nên
\(\widehat {DAB} = {180^o} - \widehat {BCD} = {60^o},\)
\(\widehat {ABC} = {180^o} - \widehat {CDA} = {100^o}.\)