Giải bài 9.9 trang 65 SGK Toán 7 tập 2 - Kết nối tri thức
Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC ( M,N không phải là đỉnh của tam giác) (H. 9.13) . Chứng minh rằng MN < BC.
Đề bài
Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC ( M,N không phải là đỉnh của tam giác) (H. 9.13) . Chứng minh rằng MN < BC.
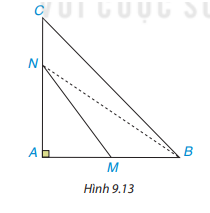
Phương pháp giải - Xem chi tiết
Sử dụng:
+ Góc tù là góc lớn nhất trong tam giác
+ Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất
Lời giải chi tiết
Ta có: Góc NMB là góc ngoài tại đỉnh M của tam giác AMN nên góc NMB là góc tù.
Góc BNC là góc ngoài tại đỉnh N của tam giác ABN nên góc BNC là góc tù.
Xét tam giác MNB có góc NMB là góc tù nên là góc lớn nhất trong tam giác. Cạnh NB đối diện với góc NMB nên là cạnh lớn nhất trong tam giác. Ta được NM < NB.(1)
Xét tam giác CNB có góc BNC là góc tù nên là góc lớn nhất trong tam giác. Cạnh CB đối diện với góc BNC nên là cạnh lớn nhất trong tam giác. Ta được NB < CB.(2)
Từ (1) và (2) ta được NM < CB.
Vậy MN < BC.