Giải bài tập 6 trang 74 SGK Toán 9 tập 2 - Cánh diều — Không quảng cáo

Đề bài

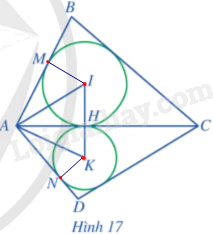
Cho tứ giác ABCD có các tam giác ABC và ACD lần lượt ngoại tiếp các đường tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn thẳng AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N (Hình 17). Chứng minh:

a) Ba điểm I, H, K thẳng hàng.

b) AM = AN.

c) \(\widehat {IAK} = \frac{1}{2}\widehat {BAD}.\)

Lời giải chi tiết

a) Do đường tròn (I) nội tiếp tam giác ABC và tiếp xúc với đường thẳng AC tại H nên \(IH \bot AC\), suy ra \(\widehat {IHA} = 90^\circ .\)

Do đường tròn (K) nội tiếp tam giác ADC và tiếp xúc với đường thẳng AC tại H nên \(KH \bot AC\), suy ra \(\widehat {IHK} = 90^\circ .\)

Ta có: \(\widehat {IHA} + \widehat {AHK} = \widehat {IHK} = 90^\circ  + 90^\circ  = 180^\circ \), nên I, H, K thẳng hàng.

b) Xét đường tròn (I) có hai tiếp tuyến AB, AC cắt nhau tại A nên AM = AH (tính chất hai tiếp tuyến cắt nhau)

Xét đường tròn (K) có hai tiếp tuyến AC, AD cắt nhau tại A nên AN = AH (tính chất hai tiếp tuyến cắt nhau)

Suy ra AM = AN ( = AH).

c) Xét đường tròn (I) có hai tiếp tuyến AB, AC nên AI là phân giác của góc BAC suy ra \(\widehat {IAH} = \frac{1}{2} \widehat {BAC}\)

Xét đường tròn (K) có hai tiếp tuyến AC, AD nên AK là phân giác của góc DAC suy ra \(\widehat {KAH} = \frac{1}{2} \widehat {DAC}\)

Ta có:

\(\widehat {IAK} = \widehat {IAH} + \widehat {KAH} \)

\(= \frac{1}{2} \widehat {BAC} + \frac{1}{2} \widehat {DAC}\)

\(= \frac{1}{2} (\widehat {BAC} + \widehat {DAC})\)

\(= \frac{1}{2}\widehat {BAD}.\)

Hay \(\widehat {IAK} = \frac{1}{2}\widehat {BAD}.\)