Giải bài tập 6 trang 79 SGK Toán 9 tập 2 - Cánh diều — Không quảng cáo

Đề bài

Khung thép của một phần sân khấu có dạng đường tròn bán kính 15m. Mắt của một người thợ ở vị trí A nhìn hai đèn ở các vị trí B, C (A, B, C cùng thuộc đường tròn bán kính 15m), bằng cách nào đó, người thợ thấy rằng góc nhìn $\widehat {BAC} = 30^\circ$ (hình 31). Khoảng cách giữa hai vị trí B và C bằng bao nhiêu mét?

Lời giải chi tiết

Bài toán được mô tả bằng hình vẽ sau:

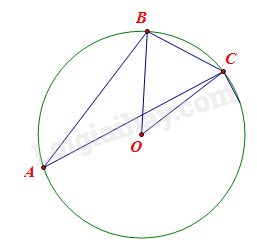
Trong đó: $\widehat {BAC} = 30^\circ ,BO = OC = R = 15m.$

Xét (O): góc BAC là góc nội tiếp chắn cung BC nên $\widehat{BAC}=\frac{1}{2}sđ\overset\frown{BC}=30{}^\circ$ do đó $sđ\overset\frown{BC}=60{}^\circ$.

Góc BOC là góc ở tâm chắc cung BC của (O) nên $\widehat{BOC}=sđ\overset\frown{BC}=60{}^\circ$.

Xét tam giác BOC có:

BO = CO (= R)

$\widehat {BOC} = 60^\circ$

Nên tam giác BOC đều

suy ra BO = CO = BC = 15m.

Vậy khoảng cách giữa B và C là 15m.