Giải bài tập 7 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo
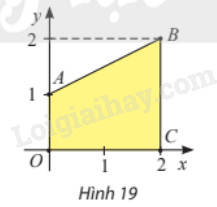
Trong mặt phẳng toạ độ (Oxy), cho hình thang (OABC) có (Aleft( {0;1} right)), (Bleft( {2;2} right)) và (Cleft( {2;0} right)) (hình dưới đây). Tính thể tích khối tròn xoay tạo thành khi quay hình thang (OABC) quanh trục (Ox).
Đề bài
Trong mặt phẳng toạ độ \(Oxy\), cho hình thang \(OABC\) có \(A\left( {0;1} \right)\), \(B\left( {2;2} \right)\) và \(C\left( {2;0} \right)\) (hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang \(OABC\) quanh trục \(Ox\).
Phương pháp giải - Xem chi tiết
Hình thang \(OABC\) được giới hạn bởi các đường thẳng \(AB\), \(OC\) (trục hoành), \(OA\) (trục tung, \(x = 0\)) và \(BC\) \(\left( {x = 2} \right)\). Phương trình đường thẳng \(AB\) là \(y = f\left( x \right) = ax + b\).
Thể tích khối tròn xoay khi quay hình thang \(OABC\) quanh trục \(Ox\) là \(V = \pi \int\limits_0^2 {{f^2}\left( x \right)dx} \)
Lời giải chi tiết
Hình thang \(OABC\) được giới hạn bởi các đường thẳng \(AB\), \(OC\) (trục hoành), \(OA\) (trục tung, \(x = 0\)) và \(BC\) \(\left( {x = 2} \right)\).
Phương trình đường thẳng \(AB\) là \(y = f\left( x \right) = ax + b\). Do \(A\left( {0;1} \right)\), \(B\left( {2;2} \right)\) nên ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{a.0 + b = 1}\\{a.2 + b = 2}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = 1\end{array} \right.\)
Vậy phương trình đường thẳng \(AB\) là \(y = \frac{1}{2}x + 1\)
Thể tích khối tròn xoay khi quay hình thang \(OABC\) quanh trục \(Ox\) là:
\(V = \pi \int\limits_0^2 {{{\left( {\frac{1}{2}x + 1} \right)}^2}dx} = \pi \int\limits_0^2 {\left( {\frac{1}{4}{x^2} + x + 1} \right)dx} = \pi \left. {\left( {\frac{{{x^3}}}{{12}} + \frac{{{x^2}}}{2} + x} \right)} \right|_0^2 = \frac{{14}}{3}\)